The +1 cellular automaton
We start with an infinite square grid
composed of empty cells.
From now on these cells will be either
empty or filled with only one of the following symbols: 0, 1, 2, 3, 4, 5, 6, 7,
8, 9, X.
The game is to place some of these
symbols wherever you want on the grid and see what they produce – “landscapes”
of numbers that evolve, loop or disappear, interesting pareidolia, the numbers
of the next lottery.
Once placed, these symbols will live
their life, driven solely by the internal laws explained below.
Start “generation #0” by sowing the
symbols you want on the grid as you wish (one symbol per cell).
In order to calculate “generation #1”,
our Automaton will now add 1 to each symbol.
So all 0s will turn into 1, all 1s into
2, all 2s into 3… and all 9s into X (we explain further what happens
to these Xs when we iterate).
Example of a simple gen#0 evolving in
gen#1 and gen #2:
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |gen#000| | | | |gen#001| | | | |gen#002| | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |
| | | | | |
| | | |
| |
| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 1
| 8 | | | | | 2 | 9 | | | | | 3 | X | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | | 0
| 6 | | | | | 1
| 7 | | | | | 2 | 8 | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 2
| 0 | 2 | 4 | | | 3 | 1 | 3 | 5 | | | 4
| 2 | 4 | 6 | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
Since an X has appeared in
a cell, the program stops adding 1 to all symbols.
It will in fact only add 1 to the 8
cells of the "crown" which surround this X (even if these
cells are completely empty). The 8 cells of the crown affected by this
operation are highlighted in aqua below.
The program erases X at
the same time – we mark in yellow (like this “X”) the exact place where X disappeared).
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |gen#003| | | | |gen#004| | | | |gen#005|
| |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 1 | 1 | 1
| |
| | 2 | 2 | 2 | | | | 2
| 2 | 2 | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
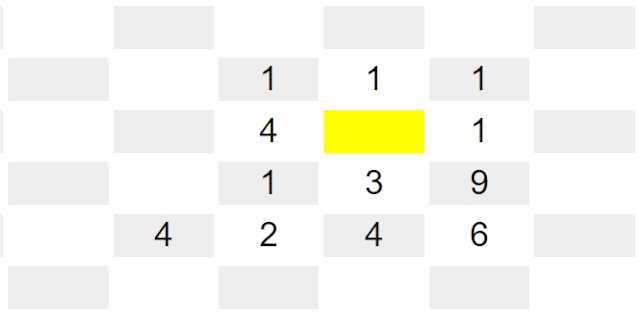
| | 4 | X | 1 | | | | 5 | | 2
| | | | 5
| 1 | 3 | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 1 | 3 | 9
| |
| | 2 | 4 | X | | | | 2
| 5 | X | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 4
| 2 | 4 | 6 | | | 5 | 2 | 5 | 7 | | | 5
| 2 | 6 |
8 | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
The iteration resumes
"normally" since no new X has appeared at gen#5. It does at gen#7 below.
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |gen#006| |
| | |gen#007|
| | | |gen#008|
| |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 3 | 3 | 3 | | | | 4
| 4 | 4 | | | | 4 | 4 | 4 | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 6
| 2 | 4 | 2 |
| | 7 | 3 | 5
| 3 | | | 7
| 3 | 5 | 3 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 3 | 6 | | 2
| |
| 4 | 7 | | 3 |
| | 4 | 8 | 1 | 4 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 6
| 3 | 7 | 9 | 2 |
| 7 | 4 | 8 | X | 3 | | 7
| 4 | 9 |
X | 4 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |
| |
| | | |
| |
| | | | | 1 | 1
| 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
Etc.
We must add one last rule, affecting the
behavior of symbols X which would be found in the crown of another symbol X.
Let us see how this new gen#0 becomes gen#1
below.
(Since there is at least one X in
the gen#0, the “natural” and general +1 rule is suspended)
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |gen#000| |
| |
| |gen#001| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | | | | | |
| | | | 1
| 1 | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 8 | 7 | X | | | | | 1 | X
| X | X | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | X | X | 5 | | |
| | 1 | X | X | 8 | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 9 | X | 8 | | |
| | 1 | X | X | X | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |
| | |
| |
| | | 1
| 1 | 1 | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |
| |
| | | |
| |
| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
The two 8s in the left diagram
above are incremented by 2 units because of the two respective Xs
touching them. They therefore transform into new Xs
(in blue in the diagram on the right).
The 7 is incremented
by 3 units because of the three Xs touching it. It also transforms
into a blue new X.
The X at the top
right (of the left diagram) will help turn the 5 into the new 8 and produce the
number 1 in its crown five times. And like all the Xs of gen#0, it
will disappear.
The 9 of the left diagram will be
transformed into a blue X because X is
the symbol which includes all sums that exceed 9.
The other 1s in the gen#1 diagram above
are easily explained.
+---+---+---+---+---+---+---+---+---+---+---+---+---+
|gen#001| |
| | | | |gen#002| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | | 1
| 1 | 1 | | | | 1 | 2 | 3 | 2
| 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 1
| X | X | | 1 |
| | | 2 | | | 1
| 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 1
| | | 8 | 1 | | | | 3 | 3 | 4 | X | 2
|
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 1
| X | | X | | | | | 2 |
| 2 | | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| | 1
| 1 | 1 | |
| | | 1 | 2 | 3 | 2
| 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |
| |
| | | |
| |
| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
The hereunder transition from gen#1 to gen#3
is explained by the same rules
+---+---+---+---+---+---+---+---+---+---+---+---+---+
|gen#002| |
| | | | |gen#003| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 1
| 2 | 3 | 2 | 1 |
| | | 1
| 2 | 3 | 2 | 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 2
| | | 1 | 1 | | | | 2 | | 1
| 2 | 2 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 3
| 3 | 4 | X | 2 |
| | | 3 | 3 | 5 | | 3
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 2
| | 2 | | 1 | | | | 2 |
| 3 | 1 | 2 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 1
| 2 | 3 | 2 | 1 |
| | | 1 | 2 | 3 | 2
| 1 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
| |
| |
| | | |
| |
| | | |
+---+---+---+---+---+---+---+---+---+---+---+---+---+
Since there are no more Xs in
gen#3, the "natural" +1 increment can be resumed in all cells that
contain a symbol. The next generations are easily calculated.
Questions
1/The very first diagram on this page (reproduced
hereunder) represents the date on which this idea germinated in the author's
head (DD/MM/YYYY format): what will become of this date at gen#100? At
gen#1000?
(below is the gen#202, computed thanks to Maximilian Hasler's page and program)
+---+---+---+---+
| |gen#000| |
+---+---+---+---+
| | 1
| 8 | |
+---+---+---+---+
| | | 0
| 6 |
+---+---+---+---+
| 2
| 0 | 2 | 4 |
+---+---+---+---+
2/ How will evolve a single 0 placed
somewhere in a blank cell of an infinite empty such grid?
(I've noticed that no zero will ever show in any gen#1 or more – no matter the gen#0)
3/ Are there configurations of symbols
that oscillate like the blinkers in Conway's Game of life? Gliders?
Guns?
______________________________
Friday 21st of June, update (sol stat)
Allan Wechsler was quick to answer and post this on Math-Fun:
AW
> This dynamic system isn't actually a cellular automaton, though the distinction may seem overly-picky and legalistic.
A cell can be in any of twelve states: 0-9, X, and blank or inactive.
The transition rule depends on whether there are any X's globally.
If there are no X's anywhere, then all the numbered cells from 0-8 go up to the next numbered state, while 9's become X's.
If there are X's, then all numbered cells are incremented by the number of adjacent X's; for this purpose, blank cells next to at least one X act as if they were in state 0. If the result is greater than 9, the cell enters state X. Finally, all X's become inactive (blank).
It is the global dependence on the existence of at least one X that makes this not be a true cellular automaton. In a CA in the strict sense, the successor state of a cell may depend only on the states of cells in a local (finite) neighborhood.
I think we can easily prove that the bounding box of active cells will grow in all directions. Look, for example, at the top line which contains active cells, and at the leftmost active cell of that row. In at most 11 generations, the cell above and to the left of it will be active.
This answers the questions about still-lifes, oscillators, and spaceships in the negative; there are no such starting configurations. Instead, every starting configuration grows without limit in all directions.
ÉA
> Merci Allan — I was suspecting something like the landscape you are describing in a very convincing way. Nevertheless, a friend of mine has just accepted to help me — I might see soon how oscillating digits could sometimes form kind of living surfaces…
« Look with all your eyes, look ! » (Verne’s Michael Strogoff)
AW
> What's possible is that you will find a set of spatially-periodic background patterns, which when extended in all directions turn out to support periodic structures superposed on them. This is what enabled Matthew Cook to discover spaceships and prove universality in the one-dimensional "rule 110".
NC
(Nicolas Graner, to whom I asked for help – and advices):
> Tout à fait d'accord avec Wechsler.
Un défaut de ton automate est qu'on n’y meurt pas assez.
Le seul cas où le nombre total de cellules vivantes diminue est quand il y a un X entouré de 8 cellules vivantes. Et même dans ce cas, la cellule laissée vide par la mort de l’X se remplira bientôt, dès qu’une de ses voisines contiendra un X.
Si tu veux des structures plus intéressantes qu’une croissance continue, il faudrait modifier les règles pour favoriser davantage la mort.
ÉA
> Oui, vous avez raison (Allan et toi) – je vais réfléchir à ça !
Maximilian Hasler (private mail)
MH
> Salut Eric !
j’ai implémenté une version très rudimentaire de ton "game of lice",
voir hasler.fr/lice.html
ÉA
.... merveille... je teste ! La date d’abord :
gen#0
gen#1
gen#2
gen#3
gen#4
gen#5
(...)
gen#10
(...)
gen#15
(...)
gen#20
(...)
gen#45
(...)
gen#70
(...)
(...)
Many thanks, Maximilian, what a wonderful tool!____________________
Hello les jeunes,
Pour ceux qui, comme le taulier, apprécient un petit tapis musical quand ils travaillent (à l’ordi et à la maison) il y a ces trois heures de techno-dub (mix 092 de Rob Jenkins après les pubs) — elles viennent de sortir (de ses machines algorithmiques) :
Sinon il y a cet autre automate [si vous connaissez un programmeur Python (ou autre), jeune, sympa (et pas trop cher) — je prends — annonce sérieuse, vraiment !-]
https://cinquantesignes.blogspot.com/2024/06/the-game-of-lice.html?m=1
Tapis musicaux ou tapis de nombres, je crois qu’on file le même coton !
Pour ceux qui, comme le taulier, apprécient un petit tapis musical quand ils travaillent (à l’ordi et à la maison) il y a ces trois heures de techno-dub (mix 092 de Rob Jenkins après les pubs) — elles viennent de sortir (de ses machines algorithmiques) :
Sinon il y a cet autre automate [si vous connaissez un programmeur Python (ou autre), jeune, sympa (et pas trop cher) — je prends — annonce sérieuse, vraiment !-]
https://cinquantesignes.blogspot.com/2024/06/the-game-of-lice.html?m=1
Tapis musicaux ou tapis de nombres, je crois qu’on file le même coton !





















Commentaires
Enregistrer un commentaire