An hexagonal seq?

I've bumped into this seq yesterday:
https://oeis.org/A214176
> Sum of the 8 nearest neighbors of n in a spiral with positive integers.
… with those beautiful graphs:
I was wondering: if we do the same on an hexagonal lattice, do we get also graphs with spikes?
If I am not wrong, the sequence would start with 27, 38, 40, 48, 56, 64… 
This is not in the OEIS.
The spiral expands like this:
_____________
Sept 23rd update
Giorgos Kalogeropoulos was quick to compute the spiral:

>Here are the first 100 terms
27, 38, 40, 48, 56, 64, 54, 78, 86, 72, 100, 84, 114, 96, 128, 108, 142, 120, 126, 162, 138, 176, 150, 156, 196, 168, 174, 216, 186, 192, 236, 204, 210, 256, 222, 228, 234, 282, 246, 252, 302, 264, 270, 276, 328, 288, 294, 300, 354, 312, 318, 324, 380, 336, 342, 348, 406, 360, 366, 372, 378, 438, 390, 396, 402, 464, 414, 420, 426, 432, 496, 444, 450, 456, 462, 528, 474, 480, 486, 492, 560, 504, 510, 516, 522, 592, 534, 540, 546, 552, 558, 630, 570, 576, 582, 588, 662, 600, 606, 612

...Thank you Giorgos – and for the beautiful graphs too (with spikes cut!-)
This will enter the OEIS soon, I hope.





























 


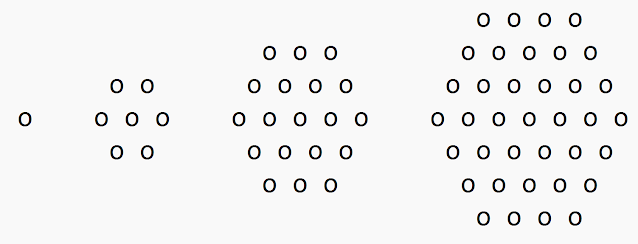
Commentaires

Enregistrer un commentaire

Posts les plus consultés de ce blog

Beautés ?

Image
Beau comme un clavier ? Un deuxième ? (celui de Modotti)   Beau comme le dos d ’ un timbre proposé par Delcampe ? Beau comme une série ukrainienne où les avions râpent le Kremlin ? Belle comme Chargois ? ... belle comme Germaine Richier ? Bel atelier ? Beau comme une pièce de 1 santim ? ... ou comme une pièce de 50  santeem ? ... Byrrh , beau comme un anus ? Beau comme la collection de Marin Karmitz à Beaubourg ? Belles Ménines ? Beau comme Marcel Duchamp ? Beau comme Jean-Luc Godard ? Beau comme la réouverture de l ’ Einsteinturm à Berlin ? Beau comme un anneau dudit ? Beau comme Eisenstein ? Beau comme les fleurs de Pascale hier matin ? Beau comme on dirait la planète Mars ? Beau comme des recherches personnelles ? Beau comme une marelle (vers le ciel) ? Beau comme un triple selfie (au Man Ray ) ? Beau comme le ciel de Sacha , mardi, en face du restaurant La Montagne ? (qui a rouvert) ... beau comme ce bleu-là de Lo ? Beau comme le froid ? Beau comme une Vespa ? Beau comme Cloon
Lire la suite

Underline, reproduce

Image
Dall.e creation If we underline the... « first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, tenth, eleventh,… » letter of this sentence S 1 , we see that the successive underlined letters simply reproduce S 1 . No big deal. If we decide not to start S 1   with "first" but with "sixth", we can reproduce the new S 6  quite easily: S 6 = sixth , second, third, fourth, fifth, first , seventh, eighth, ninth, tenth, eleventh,… S 6  was reproduced in a slightly less mechanical manner than  S 1 :  just two words of  S 1   swapped here ("first" and "sixth", in red, above). If we start S 8  with "eighth" we just swap again a pair of words of S 1  ("first" and "eighth", in red, hereunder): S 8  = eighth , second, third, fourth, fifth, sixth, seventh, first , ninth, tenth, eleventh,… What about starting S 9  with "ninth"? How many swaps do we need to reproduce S 9 ?  This is more tricky! (Indeed, we
Lire la suite

Le tripalin se présente

Image
Un tripalin est constitué de trois images. Chaque image illustre un substantif. Accolés, ces trois substantifs forment une chaîne palindromique. Laquelle nous vous invitons à trouver.  Exemple ci-dessous. Le premier mot est COL-BLEU Le second DUEL Le troisième BLOC . Ces mots forment la chaîne COLBLEUDUELBLOC qui est bien palindromique. Je posterai chaque jeudi une nouvelle salve de tripalins . Rien que des noms illustrés – pas d’adjectifs, pas de verbes conjugués, pas d’adverbes (parfois un prénom ou un nom propre – mais seulement quand il faut). À la demande générale (de mon neveu), chaque tripalin sera surmonté de son numéro d ’ ordre ( octothorpe noir) et de trois nombres bleus. Ces nombres reprennent les trois longueurs (en lettres) des trois mots présents dans le tripalin. On a par exemple ci-dessous [ #0 ↓ 7+4+4 ] car COL-BLEU comporte  7  lettres, DUEL   4  et BLOC   4 . Le numéro d ’ ordre est zéro. #0 ↓ 7+4+4 Voilà – tous retours critiques, construits ou déconstruits, bien
Lire la suite