9 frames and 1 super-frame

Hello math-Fun,

Some terminology
– say we have an infinite square grid like this:
– we put the integer 42 somewhere in a cell (we are not allowed to put more than one integer per cell):
– the cell 42 has 8 immediate neighbors
– we give the name frame to the 8 cells forming this neighborhood (highlighted in yellow hereunder):
– what is a rhyme in such a context?
– say the sum of the 8 integers (that will form in the future the frame of 42) is k
– we want k to end with the string 42 (the sum rhymes with 42 when k = 42, or 142, or 242, or 342, etc.)

The goal
We want to amaze the audience by showing them a grid filled with numbers and then asking them to pick one at random.
We show then that the sum of the eight neighbors of this number ends (graphically) with the chosen integer!

The algorithm
We start to fill the grid with a square spiral S centered on the integer 0 (zero); the constraint is to lexico-extend the spiral step by step with distinct integers rhyming with their frame.
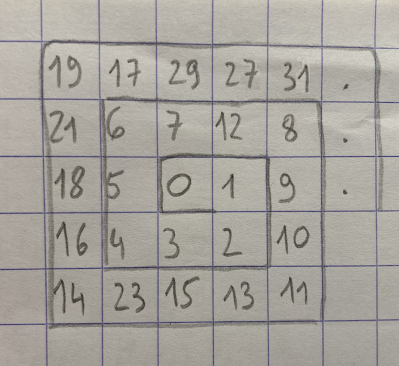
If we are correct, the first 25 terms of S are:

S = 0, 1, 2, 3, 4, 5, 6, 7, 12, 8, 9, 10, 11, 13, 15, 23, 14, 16, 18, 21, 19, 17, 29, 27, 31, ...
figure 1

If we highlight (in blue, hereunder) the frame sums of the first 9 terms, we have:
figure 2
Check
a(1) = 0 with rhyming frame sum 40 (= 1+2+3+4+5+6+7+12)
a(2) = 1 with rhyming frame sum 51 (= 9+10+2+3+0+7+12+8)
a(3) = 2 with rhyming frame sum 62 (= 10+11+13+15+3+0+1+9)
a(4) = 3 with rhyming frame sum 63 (= 2+13+15+23+4+5+0+1)
a(5) = 4 with rhyming frame sum 94 (= 3+15+23+14+16+18+5+0)
a(6) = 5 with rhyming frame sum 75 (= 0+3+4+16+18+21+6+7)
a(7) = 6 with rhyming frame sum 116 (= 7+0+5+18+21+19+17+29)
a(8) = 7 with rhyming frame sum 97 (= 12+1+0+5+6+17+29+27)
a(9) = 12 with rhyming frame sum 112 (= 8+9+1+0+7+29+25+31)
...

One question
Does this seq S extend forever (without backtracking)? We don't know – but we have the suspect that it does – all integers appearing in S sooner or later.

More terminology
What would a super-frame be?
The hereunder square spiral T shares its 16 first terms with S – then diverges; but the usual 9 frames still rhyme with their center integer.

T = 0, 1, 2, 3, 4, 5, 6, 7, 12, 8, 9, 10, 11, 13, 15, 23, 16, 14, 18, 33, 17, 39, 27, 37, 123, ... 

The purpose of this change was to form a blue super-frame, around the center integer 40 – super-rhyming with 40 (it does now, with the super-sum 840, it didn't before, with the super-sum 670):
figure 3

New first level check (arrows)
a(1) = 0 with rhyming frame sum 40 (= 1+2+3+4+5+6+7+12)
a(2) = 1 with rhyming frame sum 51 (= 9+10+2+3+0+7+12+8)
a(3) = 2 with rhyming frame sum 62 (= 10+11+13+15+3+0+1+9)
a(4) = 3 with rhyming frame sum 63 (= 2+13+15+23+4+5+0+1)
—> a(5) = 4 with rhyming frame sum 94 (= 3+15+23+16+14+18+5+0)
—> a(6) = 5 with rhyming frame sum 85 (= 0+3+4+14+18+33+6+7)
—> a(7) = 6 with rhyming frame sum 146 (= 7+0+5+18+33+17+39+27)
—> a(8) = 7 with rhyming frame sum 127 (= 12+1+0+5+6+39+27+37)
—> a(9) = 12 with rhyming frame sum 212 (= 8+9+1+0+7+27+37+123)

figure 4
Super-check
a(1) = 40 with rhyming frame sum 840 (= 51+62+63+94+85+146+127+212) 
a(2) = 51 with rhyming frame sum ... (to be continued?) 

Doubts
– Are the above 25 distinct terms of T the lexicographically earliest? (I'm quite sure they are not)
– Is it possible to fill an infinite grid with this double constraint?
Best,
É.
____________________
November 6th 2022 update
Scott S. was quick to notice that my first illustration above was not the lexicographically earliest one. He found the best possible square spiral (now in the OEIS here):
Scott:
> P.-S.
I don’t think you ever need to backtrack… my program doesn’t and it gets 10,000 terms ok. The first two terms when we start a new row or column are always the lowest two unused numbers since they do not form a 3x3 square so there is no restriction, hence all numbers will appear.

Many thanks Scott! Good job!
And if someone is interested in the lexico-first square spiral of distinct nonnegative terms producing a super-frame (or super-ring, as Scott calls it), please do not hesitate!
;-D
Best,
É.



Commentaires

Enregistrer un commentaire

Posts les plus consultés de ce blog

Beautés ?

Image
Beau comme un clavier ? Un deuxième ? (celui de Modotti)   Beau comme le dos d ’ un timbre proposé par Delcampe ? Beau comme une série ukrainienne où les avions râpent le Kremlin ? Belle comme Chargois ? ... belle comme Germaine Richier ? Bel atelier ? Beau comme une pièce de 1 santim ? ... ou comme une pièce de 50  santeem ? ... Byrrh , beau comme un anus ? Beau comme la collection de Marin Karmitz à Beaubourg ? Belles Ménines ? Beau comme Marcel Duchamp ? Beau comme Jean-Luc Godard ? Beau comme la réouverture de l ’ Einsteinturm à Berlin ? Beau comme un anneau dudit ? Beau comme Eisenstein ? Beau comme les fleurs de Pascale hier matin ? Beau comme on dirait la planète Mars ? Beau comme des recherches personnelles ? Beau comme une marelle (vers le ciel) ? Beau comme un triple selfie (au Man Ray ) ? Beau comme le ciel de Sacha , mardi, en face du restaurant La Montagne ? (qui a rouvert) ... beau comme ce bleu-là de Lo ? Beau comme le froid ? Beau comme une Vespa ? Beau comme Cloon
Lire la suite

Underline, reproduce

Image
Dall.e creation If we underline the... « first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, tenth, eleventh,… » letter of this sentence S 1 , we see that the successive underlined letters simply reproduce S 1 . No big deal. If we decide not to start S 1   with "first" but with "sixth", we can reproduce the new S 6  quite easily: S 6 = sixth , second, third, fourth, fifth, first , seventh, eighth, ninth, tenth, eleventh,… S 6  was reproduced in a slightly less mechanical manner than  S 1 :  just two words of  S 1   swapped here ("first" and "sixth", in red, above). If we start S 8  with "eighth" we just swap again a pair of words of S 1  ("first" and "eighth", in red, hereunder): S 8  = eighth , second, third, fourth, fifth, sixth, seventh, first , ninth, tenth, eleventh,… What about starting S 9  with "ninth"? How many swaps do we need to reproduce S 9 ?  This is more tricky! (Indeed, we
Lire la suite

Le tripalin se présente

Image
Un tripalin est constitué de trois images. Chaque image illustre un substantif. Accolés, ces trois substantifs forment une chaîne palindromique. Laquelle nous vous invitons à trouver.  Exemple ci-dessous. Le premier mot est COL-BLEU Le second DUEL Le troisième BLOC . Ces mots forment la chaîne COLBLEUDUELBLOC qui est bien palindromique. Je posterai chaque jeudi une nouvelle salve de tripalins . Rien que des noms illustrés – pas d’adjectifs, pas de verbes conjugués, pas d’adverbes (parfois un prénom ou un nom propre – mais seulement quand il faut). À la demande générale (de mon neveu), chaque tripalin sera surmonté de son numéro d ’ ordre ( octothorpe noir) et de trois nombres bleus. Ces nombres reprennent les trois longueurs (en lettres) des trois mots présents dans le tripalin. On a par exemple ci-dessous [ #0 ↓ 7+4+4 ] car COL-BLEU comporte  7  lettres, DUEL   4  et BLOC   4 . Le numéro d ’ ordre est zéro. #0 ↓ 7+4+4 Voilà – tous retours critiques, construits ou déconstruits, bien
Lire la suite