Tiling with digits
We all remember those "modern" clocks with their green digits. They are vintage now.
We will try though to tile an infinite grid with them – asking each digit to place itself not inside the cells of the grid but on the edges. Here is a 2 that understands what we want:
"Tiling the grid with digits" means that every "elementary grid segment" must be covered by exactly one "elementary digit segment" (the five elementary segments of the digit 2 above cover as required five elementary segments of the grid).
No overlaps are admitted (two digits 8 cannot be placed side by side as they would share at least one elementary grid segment).
In order to tile the grid, all the digits can be rotated 90 or 180 degrees (clockwise or not).
But we don't accept the digits 4 and 7 to be flipped (like in a mirror).
A last remark: two digits 1 cannot form a plus sign – but they can form a T, if they want:
And now the challenge: can you tile the infinite grid only with 1s? Only with 2s? 3s?... 9s?
The answer is yes – except with 0s and 8s, of course.
We will publish a few possible such constructions in a couple of days — and more challenges of this type. Have fun (in losing as much time as we did!-)
Feb. 26th update
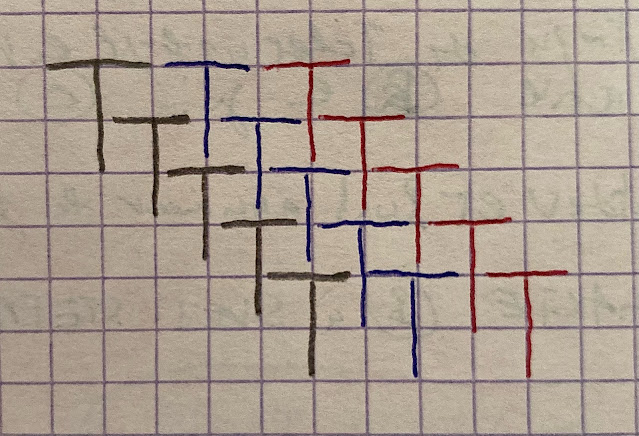
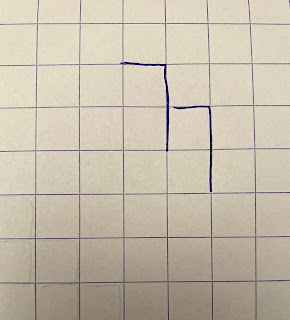
Ok, let's tile the plane with 1s; the first step is to build a diagonal of Ts:
Copy horizontaly this diagonal as many times as you want. The grid is finished:
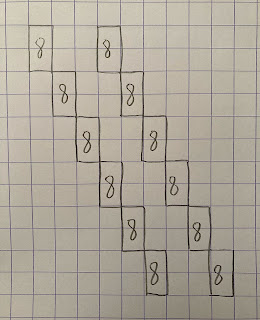
Now for the 2s; start with "the serpent":
Place an horizontal red 2 somewhere like here:This first 2 is part of another perpendicular serpent – similar to the first one:
Now copy and paste the blue and red serpents like this:
Job done! Grid tiled with 2s only!
Now for the 3s;
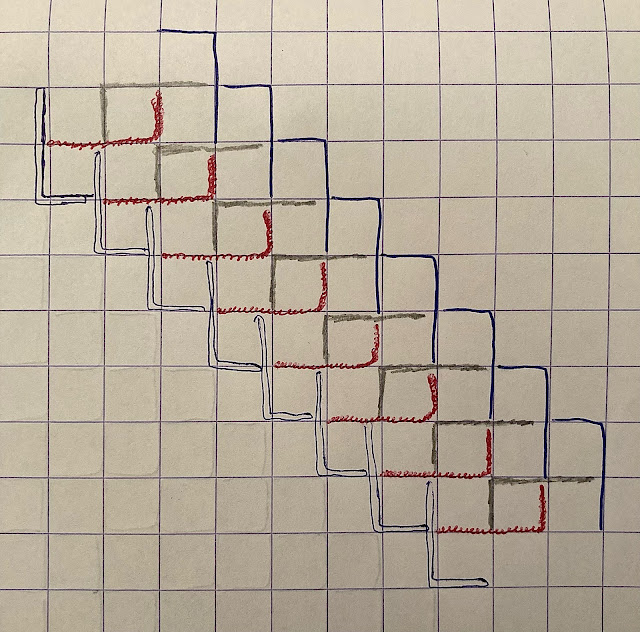
We will use here the magical "stair" technique: form a diagonal strip of stairs and copy/paste it... leaving a single-cell diagonal empty:Form a red m turning somewhere a 3 anticlockwise and step down the stairs as hereunder:
The diagonal strip is finished: leave an empty (grey) square to the right (or to the left), copy the strip, paste, repeat:
Done.
Now for the 4 (to the Floor, Thin White Duke Mix):
Assemble four 4s to produce the above "star". Glue a lot of such stars together to form our usual diagonal strip:
Copy and paste horizontaly the strips, leaving a grey empty diagonal of single squares. That's it:
Now, as a 5 is a 2 in a mirror, use the same "orthogonal serpents" technique for the 5s (as seen above).The 6s are easy to handle as our usual "diagonal strip" appears almost immediately:
The 7 looks like an easy shape; it's not obvious to assemble them, though. To get our usual diagonal strip, you must first glue together four diagonals of 7s – properly turned clockwise or anticlockwise:[8s (or 0s) cannot tile the plane, and 9s are rotated 6s].
Here are a few tiling-the-grid kleinigkeiten (using not single digits but two or more of them).
A tiling with 1s and 4s, for instance:
The 8+2 tiling uses the other diagonal:
We've not used them yet, but horizontal (or vertical) strips are sometimes useful. Here is how you might use the digits 1 to 5 together to tile the grid:
You can put on top of the above 4-3-2-4 strip one of the three horizontal strips hereunder...
... and at the bottom of the 4-3-2-4 strip a line of 1s.
You glue under this horizontal line of 1s another infinite 4-3-2-4 strip, and so on.
Question:
Who will be the first to tile the grid with the smallest repeated pattern that uses all the digits from 1 to 9?
_________________
Feb 27th update
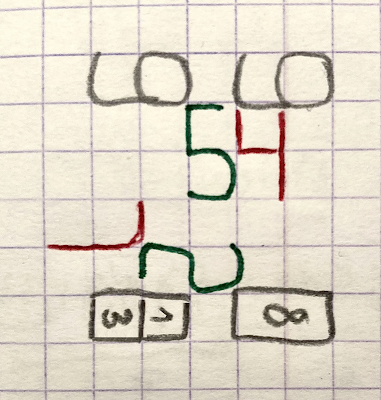
It is possible (with a little trick) to tile the grid with a 3 x 6 regular pattern that shows the integers 1 to 9; here is how the 9 digits are placed in the tile A:
On top we have a 6 and a 9 (same shape, but rotated);
the bottom shows two 8s: a genuine one and a 1 + 3 one!
If we admit that the "8" shape presents 1, 3 and 8 (and why not 0!) and that the "9" shape presents 6 and 9, we can cut vertically in half our tile A (the pink vertical rectangle).
If we turn the pink rectangle 90 degrees anticlockwise and stack a pile of such 5 half-A patterns, we get this:
We will now copy this stack and paste it on the left of itself – with a small shift of two cells up (the top right corner of an "8" touching the bottom left corner of the 6/9 cell); here is how 6 pink horizontal rectangles will tile the grid:
If you've understood this gibber, let me know!-)





































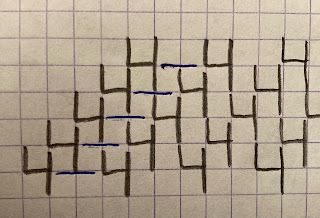








.jpeg)









Commentaires
Enregistrer un commentaire