More and more spiral stuff (with a few hand-woven grids)

The idea is to fill the cells of an infinite 2D lattice grid with integers that don’t share any digit with their surrounding 8 cells. To do that we start with a zero somewhere and develop a square spiral S, always extending S with the smallest possible term not yet used (that doesn’t lead to a contradiction). Questions: will S stop at some point? Could S be infinite if some backtracking is accepted?

[Hereunder is my (almost) original e-mail in French to Carole, explaining why the above 9 is followed by 30 and 44]:

>> Alors voilà, >> on enroule une spirale S autour de zéro, >> comme d’habitude, en l’étendant avec >> le plus petit terme T absent de S — de >> manière à ce qu’aucun des chiffres de T >> ne soit présent dans son voisinage V. >> Ce V est fait des 8 cases qui entourent T. >> On enroule facilement les nombres qui >> vont de 0 à 9.

>> Mais le suivant, A, demande un calcul : >> A ne peut commencer par 1 (à cause >> du « 1 » dans son V), ni par 2 (à cause >> du « 2 ») ; en revanche il peut commencer

>> par 3 — comme dans 30 — et vu qu'il n’y

>> a aucun 0 actuellement dans le V de 30,

>> on garde ce 30 ; on le met ici sous le 9

>> de S. >> >> Le terme suivant ne peut commencer ni >> par 1, ni par 2, ni par 3 — mais 4 est ok. >> Les termes 40, 41, 42 et 43 sont interdits,

>> évidemment, mais 44 convient. >> >> Sous 44 on placera de même 10, le plus

>> petit absent de S qui n’a ni 0 ni 1 dans

>> son V à ce stade. >> Etc. >> >> Je croyais que S s’arrêterait rapidement — >> je vois qu’il n’en est rien ! >> J’ai déjà ce début pour S (attention, fait

>> en 10 minutes d’un seul jet) : >> S = 0,1,2,3,4,5,6,7,8,9,30,44,10,55,11,

20,13,66,12,34,24,22,15,23,16,24,57,18,25,

36,27,48,26,34,56,47,28,50,49,58,60,27,35,

66,37,40,77,59,38,17,69,…

>> Question : ça bloquera quand ?!

>> Qu’en penses-tu ? C joli une grille carrée >> remplie de nombres qui ne partagent aucun >> chiffre avec leur voisinage immédiat, non ?

>> à+

>> É.

[Carole, this morning]:

Je confirme !
S = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 30, 44, 10, 55, 11, 20, 13, 66, 12, 33, 14, 22, 15, 23, 16, 24, 57, 18, 25, 36, 27, 48, 26, 34, 56, 47, 28, 50, 49, 58, 60, 29, 35, 67, 38, 40, 77, 59, 37, 19, 68, 39, 46, 70, 41, 80, 31, 65, 90, 17, 88, 21, 93, 51, 43, 69, 71, 32, 111, 73, 81, 64, 72, 89, 42, 91, 52, 61, 82, 400, 62, 45, 300, 54, 100, 85, 92, 53, 76, 94, 75, 200, 74, 83, 222, 63, 404, 78, 202, 79, 86, 101, 225, 84, 95, 406, 99, 205, 333, 98, 103, 444, 105, 336, 87, 303, 97, 335, 117, 338, 107, 96, 228, 116, 227, 339, 446, 110, 448, 102, 383, 106, 223, 449, 113, 555, 109, 445, 118, 229, 115, 334, 151, 203, 114, 557, 343, 666, 130, 272, 131, 777, 141, 667, 224, 556, 242, 778, 226, 779, 244, 119, 245, 161, 204, 669, 252, 4444, 232, 104, 575, 304, 559, 408, 155, 277, 353, 676, 595, 447, 599, 474, 108, 565, 700, 262, 477, 233, 677, 330, 464, 707, 266, 787, 696, 558, 206, 393, 208, 191, 255,...

_________________________________________________________________________________________________________

The above 2D square lattice was produced again with the help of a spiral S centered on 0. The idea, here, is to form a "level 2" spiral Z (made by the the dark blue small numbers "z" at every intersection), such that any "z" is always the sum of the 4 integers inside the 2x2 square 'beneath' it and z(k) shows (as a substring) the kth term of S.

Example:

The blue spiral Z starts with 10:

Z(1) = 10 as the sum 0+1+2+7 = 10 and 10 has the opening 0 of the red spiral S as a substring;

Z(2) = 14 as the sum 0+7+3+4 = 14 and 14 has S(2) = 1 as a substring;

Z(3) = 20 as the sum 0+4+5+11 = 20 and 20 has S(3) = 2 as a substring;

...

Last example (in the lower right 2x2 square):

Z(21) = 116 as the sum 9+46+41+20 = 116 and 116 has S(21) = 16 as a substring (the original 16 is in the upper left corner of the red spiral); etc.

We see that the spiral Z embeds the spiral that produced Z itself.

[Hereunder is my second e-mail in French to Carole, explaining how S was built]

Le 1er terme de la spirale S est visible dans la sommes des termes du 1er carré 2x2 (0 est dans 10) ;

Le 2e terme de la spirale S est visible dans la sommes des termes du 2e carré 2x2 (1 est dans 14) ;

Le 3e terme de la spirale S est visible dans la sommes des termes du 3e carré 2x2 (2 est dans 20) ;

Le 4e terme de la spirale S est visible dans la sommes des termes du 4e carré 2x2 (7 est dans 27) ;

Le 5e terme de la spirale S est visible dans la sommes des termes du 5e carré 2x2 (3 est dans 30) ;

Le 6e terme de la spirale S est visible dans la sommes des termes du 6e carré 2x2 (4 est dans 24) ;

Etc.

La suite « Spi dans Spi » commence ainsi (caveat habituel) : SdS = 0,1,2,7,3,4,5,11,15,6,8,13,9,10,91,14,12,17,

24,80,16,18,67,98,21,19,66,37,112,46,20,41,58,…

[update, May 27th]

Here are Carole's results, correcting mine:

SdS = 0, 1, 2, 7, 3, 4, 5, 11, 15, 6, 8, 13, 9, 21, 80, 25, 10, 18, 23, 81, 12, 31, 74, 180, 24, 14, 56, 48, 54, 105, 16, 82, 19, 154, 921, 68, 17, 45, 83, 124, 26, 931, 20, 53, 86, 28, 872, 845, 85, 22, 49, 126, 153, 869, 98, 712, 27, 65, 90, 95, 60, 737, 119, 181, 29, 195, 92, 906, 40, 679, 62, 699, 30, 78, 114, 37, 44, 116, 904, 285, 789, 32, 186, 938, 79, 548, 70, 642, 110, 850, 33, 120, 66, 893, 59, 130, 189, 859, 1126, 453, 34, 216, 746, 905, 76, 526, 125, 776, 573, 1548, 35, 220, 792, 182, 560, 118, 852, 317, 353, 9699, 933, 36, 133, 865, 757, 131, 218, 690, 723, 301, 312, 10353, 38, 111, 956, 650, 211, 397, 532, 1001, 268, 100, 8020, 426, 39, 137, 943, 960, 146, 183, 433, 606, 1216, 445, 554, 8216, 41, 46, 809, 135, 541, 827, 892, 670, 8171, 427, 521, 6867, 590, 42, 71, 897, 1048, 290, 282, 552, 973, 1220, 8972, 860, 1029, 6796, 43, 64, 233, 509, 1020, 660, 559, 404, 733, 6169, 890, 511, 7910, 215, 47, 121, 174, 643, 7934,...

Comme d’habitude SdS est la lexicographically première de termes

distincts non négatifs.

_________________________________________________________________________________________________________

A variant (see the diagram above): Z(k) must start with S(k) — as opposed to embed, seen above; S must be the lexicographically earliest sequence of distinct terms > 0 [thus S(1) = 1] and, as seen before, Z must be the sum of the four integers of the 2x2 square 'beneath' it. The terms of S grow quickly, of course.

Example:

S(1) = 1 (red spiral) and Z(1) = 10 (blue spiral) as 10 is the sum 1+2+3+4 'beneath" Z(1) and 10 starts with 1;

S(2) = 2 (red spiral) and Z(2) = 20 (blue spiral) as 20 is the sum 1+4+5+10 'beneath" Z(2) and 20 starts with 2;

S(3) = 3 (red spiral) and Z(3) = 30 (blue spiral) as 30 is the sum 1+10+6+13 'beneath" Z(3) and 30 starts with 3;

S(4) = 4 (red spiral) and Z(4) = 40 (blue spiral) as 40 is the sum 1+13+24+2 'beneath" Z(4) and 40 starts with 4;

S(5) = 5 (red spiral) and Z(5) = 50 (blue spiral) as 50 is the sum 2+24+7+17 'beneath" Z(5) and 50 starts with 5;

S(6) = 10 (red spiral) and Z(6) = 100 (blue spiral) as 100 is the sum 2+17+78+3 beneath" Z(6) and 100 starts with 10;

...

Another (and last) example:

The above right 2x2 square (at the end of the red spiral) leads to Z(17) being 900000 = 120180+12+7+779801 [the sum of the four integers 'beneath' Z(17)] as Z(17) must be the smallest available integer of the blue spiral beginning with 9 [= S(17)], this 9 being in the lower left square of the red spiral.

[in French to Carole again]:

Là, les nombres de la suite d’origine croissent vite (sauf erreur — et début avec 1 comme signalé

dans mon e-mail précédent) :

ScS = 1,2,3,4,5,10,6,13,24,7,17,78,8,511,782,1609,9,

5377,11608,66376,11,13607,37474,40689,120180,

12,779801,…

_______________________________________________________________________________________________

Another variant (above): Z(k) must end with S(k) — as opposed to embed or begin, seen before. S must be the lexicographically earliest sequence of distinct terms > 0 [thus S(1) = 1] and, as seen before, Z must be the sum of the four integers of the 2x2 square 'beneath' it.

Example:

S(1) = 0 (red spiral) and Z(1) = 10 (blue spiral) as 10 is the sum 0+1+2+7 'beneath" Z(1) and 10 ends in 0;

S(2) = 1 (red spiral) and Z(2) = 21 (blue spiral) as 20 is the sum 10+1+5+4 'beneath" Z(2) and 21 ends in 1;

S(3) = 2 (red spiral) and Z(3) = 32 (blue spiral) as 32 is the sum 0+11+4+17 'beneath" Z(3) and 32 ends in 2;

S(4) = 7 (red spiral) and Z(3) = 27 (blue spiral) as 27 is the sum 0+17+9+1 'beneath" Z(3) and 27 starts in 7; etc.

...

Another (and last) example:

The upper right 2x2 square (of the red spiral) leads to Z(17) being 110 = 28+13+64+5 [the sum of the four integers 'beneath' Z(17)] as Z(17) must be the smallest available integer of the blue spiral ending in 10 [= S(17)], this 10 being in the lower left square of the red spiral.

[in French to Carole again]:

… et ici la SfS — où la spirale d’origine _termine_ la

spirale « des sommes 2x2 » de niveau supérieur :

SfS = 0,1,2,7,3,11,4,17,9,5,8,100,6,16,92,27,10,15,19,

1066,12,14,81,85,28,13,64,38,73,887,15,104,88,… Près du coin inférieur droit (illu) il y a une somme 1066

(au bic) intéressante en ce qu’elle est _identique_ au

terme correspondant de la spirale (le terme 1066 au

crayon en haut à G de la spirale), ce qui est légal, bien

sûr !

_______________________________________________________________________________________________

The above spiral is the last one of the day: the succession of the digits of S is the same as the succession of the digits of Z.

And Z(k) is, as always, the sum of the terms in the 2x2 square 'beneath' Z(k).

Example:

– the first 2x2 formed by S has sum 12 = 12+2+3+6, and this 12 comes from S(1)=1 and S(2)=2 (red spiral);

– the second 2x2 formed by S has sum 36 = 1+6+4+25, and this 36 comes from S(3)=3 and S(4)=6 (red spiral);

– the third 2x2 formed by S has sum 42 = 1+25+5+11, and this 42 comes from S(5)=4 and the first digit of S(6)=25 (red spiral);

Look at the seqs S and Z (on top of each other hereunder): the digit-succession is the same in both seqs:

S = 1,2,3,6,4,25,5,11,41,7,64,107,8,292,481,433,9,368,...

Z = 12, 36, 42, 55, 114,176,410,782, 924,814,3393,...

And our last e-mail in French to Carole:

Hello Carole,

Spi5 = 1,2,3,6,4,25,5,11,41,7,64,107,8,292,481,433,9,368,…

Sommes=12,36,42,55,114,176,410,782,924,814,3393,…

Les deux successions de chiffres sont identiques (modulo erreurs).

_______________________________________________________________________________________________

The above green-arrows-spiral, or another update, Friday 28th, May 2022

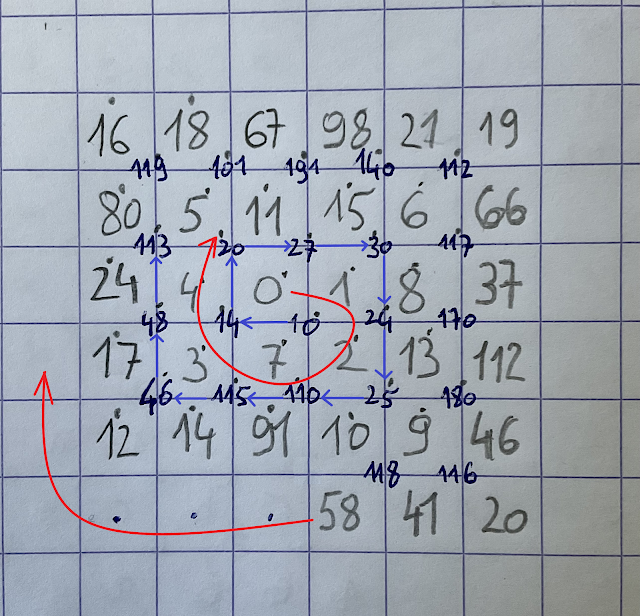
On an infinite square grid we put a distinct integer A in every cell such that at least one of the digits of A is present in the vertical sum of the 3-term segment N-A-S, and at least one of the digits of A is present in the horizontal sum of the 3-term segment O-A-E (might be the same digit of A, or another one of A).

Example:

– we have above S(1)=0, S(2)=1, S(3)=2, S(4)=3, S(5)=8... and this 8 is a substring of both 38 (=27+8+3) and 58 (=9+8+11);

– two squares above 8 we have S(7)=12; the 1 of 12 is a substring of 105(=86+12+7) and the 2 of 12 is a substring of 32 (=11+12+9).

Variant #1 is when we consider a cross in the shape of 'X' instead of the above shape '+' and

Variant #2 is when we superpose 'X' and '+' and consider the 4 sums in which A is embedded.

In French:

Hello Carole,
G eu cette idée aussi :
sur une lexico-grille carrée avec des

nombres distincts (comme tu connais)
on peut imaginer la règle suivante :
— tout nombre A est au centre d’une
« croix » composée des 4 nombres
qui lui sont collés horizontalement
et verticalement [illu : le nombre A
est collé à N (nord), E (est), S (sud) et
O (ouest)] ;
— nous exigeons qu’un des chiffres
de A se retrouve dans O+A+E mais
aussi dans N+A+S (ça peut être un
chiffre de A différent).
Voilà. On construit la grille à l’aide
d’une lexico-spirale classique.
— Ainsi le zéro central de l’illu [c’est
donc S(1)] est il dans 9+0+1 = 10
et dans 7+0+3 = 10 aussi.
Dernier exemple :
— Le 12 en haut à gauche de l’illu
est au centre d’une croix dont la
branche horizontale vaut 105
(=86+12+7) : ce 105 contient bien
le « 1 » de 12, alors que la branche
verticale vaut 32 (=11+12+9),

lequel 32 contient bien le « 2 » de 12.
Cette SpiBoussole est une permutation
des non-négatifs.

La variante /1/ évidente est celle où
l’on ne considère pas une croix en
forme de « + » comme ici, mais une
croix en forme de « x ».

La variante /2/ combine « + » et « x ».
Ça doit être monstrueux !-))

Ma lexico-SpiBoussole doit être très
rapidement bancale, pardon — la voici :
quand même :

SB = 0,1,2,3,8,9,12,7,18,6,10,15,16,17,28,41,5,27,40,

86, 20,11,30,19,40,21,22,29,42,31,38,25,…

Bancale, en effet — je vois que le 40 à

la fin de la 1re ligne doit être remplacé

par 20, faussant ainsi le reste de la spirale...

Encore raté, caramba !

__________________________________________________________________________________

Update by Carole and corrections; this is the new SB sequence(which we will call S+ from now on) and the corresponding blue spiral of the corrected above "cross sequence"; its precise definition is:

—> any "+" shape formed by 5 terms has an integer A in its center such that at least one digit of A is present in the sum of the 3-horizontal bar integers of the "+" shape AND at least one digit of A is also present in the sum of the 3-vertical integers of the same "+" shape (the digits can differ or be the same, see the Example below):

S+ = 0, 1, 2, 3, 8, 9, 12, 7, 18, 6, 10, 15, 16, 17, 28, 41, 5, 27, 20, 13, 4, 11, 66, 19, 30, 14, 22, 89, 37, 31, 23, 25, 54, 55, 42, 24, 26, 29, 35, 21, 36, 39, 34, 32, 58, 63, 44, 47, 73, 33, 40, 74, 50, 51, 46, 45, 43, 38, 82, 64, 68, 49, 75, 61, 48, 52, 56, 53, 76, 57, 92, 65, 59, 60, 67, 69, 103, 71, 77, 126, 62, 70, 87, 80, 81, 117, 72, 79, 78, 113, 90, 85, 107, 95, 88, 105, 98, 86, 83, 84, 91, 99, 104, 100, 97, 110, 94, 93, 96, 106, 101, 111, 102, 108, 109, 114, 122, 146, 116, 119, 144, 118, 115, 128, 138, 123, 112, 127, 132, 124, 125, 133, 120, 136, 129, 130, 121, 131, 134, 135, 145, 137, 148, 139, 142, 140, 143, 147, 149, 141, 154, 153, 150, 155, 151, 159, 161, 163, 191, 156, 165, 181, 164, 168, 178, 169, 170, 167, 175, 158, 152, 171, 174, 162, 160, 182, 172, 157, 179, 173, 166, 176, 177, 187, 184, 180, 186, 185, 192, 194, 183, 196, 190, 193, 188, 197, 189, 195, 198, 199, 200, ...

Example (consider the S+ corresponding blue spiral hereafter):

–> S+(1) = the initial 0 is present in the 3-term horizontal sum 10 (=9+0+1) AND in the same 3-term vertical sum 10 (=7+0+3);

—> S+(9) = 18 has its digit "1" present in the 3-term horizontal sum 31 (=7+18+6) AND its digit "8" present in the 3-term vertical sum 38 (=19+18+1);

__________________________________________________________________________________

Now for the...

Variant #1 (we look at the X shape sums instead of the + sums):

SX = 0, 1, 2, 3, 4, 5, 8, 6, 16, 7, 9, 10, 18, 15, 11, 19, 20, 14, 25, 17, 30, 29, 35, 45, 40, 39, 28, 26, 24, 49, 21, 13, 36, 46, 38, 27, 48, 12, 22, 31, 23, 50, 32, 34, 52, 33, 42, 43, 44, 37, 41, 56, 60, 79, 51, 55, 53, 63, 59, 61, 72, 73, 54, 66, 70, 65, 76, 62, 78, 67, 64, 58, 68, 69, 105, 57, 47, 71, 129, 75, 80, 77, 74, 81, 82, 91, 88, 87, 83, 101, 84, 85, 94, 108, 95, 93, 92, 115, 102, 103, 86, 89, 98, 114, 136, 90, 118, 128, 97, 100, 96, 106, 99, 135, 138, 104, 125, 113, 116, 107, 124, 123, 109, 143, 110, 120, 119, 132, 137, 117, 134, 144, 111, 127, 126, 112, 122, 130, 121, 140, 131, 133, 139, 141, 142, 145, 155, 166, 150, 152, 146, 156, 162, 185, 148, 147, 165, 151, 175, 154, 172, 149, 158, 153, 160, 157, 161, 159, 167, 163, 168, 169, 178, 170, 186, 171, 190, 173, 164, 174, 176, 177, 196, 179, 194, 181, 200, 184, 197, 180, 198, 182, 187, 183, 188, 189, 191, 192, 199, 201, 204,...

The blue spiral corresponding to the X-shape sums is hereunder:

Example:

– SX(1) = 0; the initial 0 is present in the 3-term diagonal sum "/" 20 (=16+0+4) AND in the other 3-term diagonal "\" sum 10 (=8+0+2);

— SX(12) = 10 has its digit "1" present in the 3-term diagonal sum "/" sum 51 (=26+10+15) AND its digit "0" present in the 3-term diagonal "\" sum 60 (=1+10+49); etc.

__________________________________________________________________________________

Now for the...
Variant #2 (we look both at the X shape sums and the + shape sums): 

SX+ = 0, 1, 2, 3, 8, 9, 78, 7, 12, 6, 10, 97, 20, 18, 30, 269, 40, 73, 50, 82, 49, 70, 60, 131, 80, 19, 28, 79, 68, 69, 58, 63, 62, 4, 48, 34, 22, 5, 26, 31, 43, 29, 17, 13, 92, 23, 98, 72, 46, 16, 14, 51, 81, 24, 87, 27, 11, 25, 90, 134, 100, 272, 56, 35, 59, 67, 130, 66, 140, 107, 44, 83, 21, 32, 39, 61, 41, 109, 101, 71, 38, 74, 42, 84, 52, 36, 142, 115, 93, 75, 37, 33, 167, 76, 53, 64, 47, 136, 146, 65, 15, 45, 85, 165, 164, 135, 153, 168, 137, 77, 103, 57, 193, 86, 203, 88, 293, 108, 102, 54, 129, 55, 128, 89, 151, 174, 96, 99, 199, 117, 111, 113, 91, 95, 119, 127, 191, 161, 184, 138, 110, 143, 112, 106, 94, 132, 144, 105, 121, 126, 114, 163, 139, 133, 149, 147, 116, 148, 157, 120, 123, 171, 179, 189, 200, 231, 122, 118, 172, 124, 141, 185, 154, 166, 198, 177, 298, 284, 268, 125, 187, 145, 162, 197, 213, 207, 237, 192, 152, 159, 104, 155, 156, 175, 160, 169, 150, 190, 173, 215, 225,

The blue spiral corresponding to the Xand+ shape sums is hereunder:

Example:

– SX+(1) = 0; the initial 0 is present in the 3-term horizontal sum 10 (=9+0+1) AND in the same 3-term vertical sum 10 (=7+0+3) AND in the 3-term diagonal "/" sum 20 (=12+0+8) AND in the 3-term diagonal "\" sum 80 (=78+0+2);

— SX+(46) = 23 (locatedv3 cells on top of the initial 0 in the blue spiral above) and 23 has its digit "2" (and also "3") present in the 3-term horizontal sum 213 (=92+23+98) AND the same its digit 2 again in the 3-term vertical sum 124 (=41+23+60) AND MORE, the digit 2 of 23 is in the 3-term diagonal "/" that sums up to 202 (=109+23+70) AND in the 3-term diagonal "\" that sums up to 215 (=61+23+131); etc.

______________________________________________________________________________________________________

Another update (May 29th) with this beautiful spiral by Scott Shannon (explanation below the picture – click it to enlarge):

Both the sum of the four integers inside a 2x2 "box" and the sum of the digits inside the same box are square numbers – waooow!

Example:

– the 1st box with the 0 contains the 4-term sum 25 (=0+1+19+6) and the digit-sum 16 (=0+1+1+9+6), which are two squares;

– the "a" box contains the 4-term sum 169 (=2+25+141+1) and the digit-sum 16 (=2+2+5+1+4+1+1), which are two squares;

– the "b" box contains the 4-term sum 144 (=19+8+26+91) and the digit-sum 36 (=1+9+8+2+6+9+1), which are two squares;

– the "pink arrow" box contains the 4-term sum 169 (=4+5+29+131) and the digit-sum 25 (=4+5+2+9+1+3+1), which are two squares; etc.

Scott's spiral produces the hereunder sequence Z (now in the OEIS as A354111):

Z = 0, 1, 2, 6, 3, 7, 4, 5, 19, 8, 141, 25, 9, 133, 28, 132, 10, 24, 135, 23, 11, 131, 29, 91, 26, 12, 98, 378, 32, 78,13, 44, 39, 124, 157, 230, 14, 275, 220, 105, 178, 229, 15, 69, 365, 51, 54, 153, 385, 16, 163, 303, 62, 104, 227, 123, 17, 43, 476, 66,212, 83, 106, 134, 18, 30, 210, 195, 56, 102, 647, 265, 20, 276, 481, 241, 72, 48, 321, 41, 399, 21, 140, 257, 1041, 358, 52, 58, 33, 268,22, 422, 94, 228, 71, 92, 342, 45, 156, 421, 27, 263, 418, 638, 806, 879, 119, 221, 716, 520, 31, 390, 214, 185, 249, 279, 226, 305, 629, 867,649, 34, 1060, 460, 232, 234, 576, 170, 161, 324, 819, 47, 35, 337, 308, 1201, 502, 720, 206, 260, 82, 558, 309, 143, 36, 118, 748, 420, 373, 299,1985, 42, 59, 300, 1065, 148, 37, 108, 371, 114, 63, 128, 500, 439, 186, 996, 757, 976, 277, 38, 492, 1015, 381, 223, 607, 432, 266, 559, 805, 261,317, 330, 40, 495, 1342, 717, 478, 955, 527, 311, 519, 295, 1874, 68, 636, 1210, 46, 472, 103, 120, 233, 270, 994, 691, 1003, 192, 893, 446, 190, 201,49, 154, 142, 900, 136, 416, 122, 211, 146, 70, 684, 479, 389, 959, 95, 50, 658, 928, 701, 207, 710, 224, 501, 322, 702, 1070, 568, 703, 171, 188,53, 160, 205, 167, 799, 1031, 240, 127, 331, 360, 1035, 892, 191, 1314, 440, 329, 55, 726, 605, 116, 145, 591, 202, 383, 741, 269, 745, 286, 491, 722,183, 1331, 57, 772, 181, 252, 470, 1198, 3150, 281, 410, 529, 96, 306, 467, 601, 860, 1930, 1646, 60, 948, 1369, 1141, 366, 575, 357, 918, 121, 80, 417,115, 456, 1298, 532, 553, 362, 61, 253, 434, 290, 179, 4939, 1152, 493, 296, 87, 666, 643, 1151, 902, 297, 158, 517, 255, 64, 782, 3478, 1591, 392, 791, ...

______________________________________________________________________________________________________

Another wonderful task performed by Maximilian H. this morning (May the 30th, 2022):

—> The same sequence W (of distinct nonnegative terms, lexicographically) forms both a spiral S1 filling an infinite 2D square grid G1 and the antidiagonals of an infinite array A1 (tiling the South-East 1/4 of a 2D square grid), in such a manner that any 2x2 "box" of G1 and of A1 contains 4 terms whose sum is a square!

Example1: we see that the above 2x2 box in the down left corner (with integers 25189, 13, 36, 43) has a square sum when we add the said integers: 25189+13+36+43=25281 (=159^2);

Example2: we see that the above 2x2 box in the down right corner (with integers 2, 375, 20, 1628) has a square sum when we add the said integers: 2+375+20+1628=2025 (=45^2); etc.

BUT we see hereunder that if the same sequence W sows its terms along the antidiagonals of a 1/4 grid (successive red arrows) we get different 2x2 "boxes" (next illustration):

Example3: we see that the above 2x2 blue box in the upper left corner (with integers 0, 1, 13, 2) has a square sum when we add the said integers: 0+1+13+2=16;

Example4: we see that the next 2x2 blue box in the center (with integers 16, 375, 20, 25189) has a square sum when we add the said integers: 16+375+20+25189=25600 (=160^2); etc. Bravo Maximilian, this is a hell to compute (due to the backtracking).

This is a draft now (in the OEIS) but will be soon a full entry.

______________________________________________________________________________________________________

Carole has just proposed this now (does she sleep sometimes?-):

Any horizontal ABC or vertical XYZ alignment of 3 neighboring terms has a square sum:

S3+sq = 0, 1, 2, 3, 4, 8, 13, 22, 46, 32, 24, 44, 53, 6, 166, 312, 51, 18, 892, 3446, 151, 15, 59, 122, 3788, 186, 43, 171, 75, 8590, 360, 47, 617, 120, 43784, 137572, 973, 37, 14, 19549, 4462, 5918, 229, 124, 872, 448, 616, 536, 612, 77, 251, 15801, 589, 16010, 1357, 322, 85, 266, 15525, 338, 36578, 88400, 362226, 69215, 208, 584, 108, 2672,...

Example:

The initial 0 above is horizontally aligned with 8 and 892 and 0+8+892=900 (square of 30);

but 0 is also aligned with 8 and 1: 8+0+1=9;

and 0 is aligned with 1 and 24: 0+1+24=25.

Vertically, we have three more alignments:

0+3+166=169 (square of 13);

22+0+3=25;

59+22+0=81; etc.

Carole has performed the same task hereunder – but with the constraint "prime sum" instead of "square sum". The definition of the S3+pr sequence is:

«Spiral on a 2D square lattice, one term per cell, starting at the origin with 0; any horizontally or vertically aligned and neighboring cells add up to a prime»:

S3+pr = 0, 1, 2, 3, 6, 4, 7, 8, 14, 9, 10, 12, 15, 16, 28, 27, 18, 20, 33, 26, 24, 30, 5, 32, 22, 13, 36, 48, 17, 42, 38, 34, 11, 52, 40, 21, 46, 44, 41, 64, 68, 19, 50, 23, 66, 60, 25, 72, 54, 31, 62, 56, 39, 78, 74, 29, 70, 47, 82, 100, 51, 90, 58, 49, 84, 96, 77, 120, 114, 37, 88, 108, 43, 80, 104, 55, 92, 94, 85, 132, 130, 45, 106, 76, 57, 124, 102, 81, 166, 112, 35, 98, 138, 75, 118, 154, 111, 144, 128, 59, 126, 136, 69, 142, 156, 61, 172, 116, 65, 208, 86, 160, 67, 204, 148, 87, 162, 190, 91, 150, 180, 53, 174, 140, 95, 198, 168, 83, 122, 178, 89, 220, 110, 134, 73, 146, 202, 113, 184, 152, 151, 176, 164, 117, 158, 182, 93, 188, 242, 133, 226, 210, 127, 186, 228, 107, 206, 79, 194, 170, 123, 216, 218, 153, 192, 196, 99, 214, 234, 109, 200, 212, 175, 230, 236, 97, 224, 296, 213, 248, 266, 63, 240, 71, 252, 278, 147, 222, 232, 165, 246, 262, 105, 264, 244, 139, 258, 272, 101, 270, 290,...

Example:

The initial 0 above is horizontally aligned with 33 and 4 and 33+4+0=37 (a prime);

but 0 is also aligned with 4 and 1: 4+0+1=5;

and 0 is aligned with 1 and 10: 0+1+10=11.

Vertically, we have three more alignments:

0+3+28=31 (a prime again);

8+0+3=11;

5+8+0=13; etc.

The same idea – but with both diagonal alignments "/" and "\" adding up to a prime:

S3Xpr = 0, 1, 2, 3, 4, 5, 9, 6, 7, 13, 8, 10, 11, 15, 19, 25, 27, 12, 14, 21, 20, 16, 38, 18, 22, 17, 31, 28, 26, 30, 24, 23, 36, 34, 32, 33, 40, 42, 44, 46, 29, 35, 50, 37, 52, 66, 54, 43, 60, 41, 58, 71, 114, 48, 39, 49, 62, 45, 76, 78, 80, 64, 56, 51, 70, 47, 55, 82, 102, 79, 84, 53, 57, 74, 59, 65, 91, 67, 75, 88, 69, 73, 68, 94, 93, 61, 118, 63, 72, 100, 77, 81, 99, 85, 111, 96, 83, 95, 103, 89, 87, 90, 98, 101, 132, 109, 105, 144, 86, 123, 92, 112, 128, 150, 124, 131, 134, 148, 104, 108, 110, 97, 107, 166, 140, 142, 106, 139, 117, 130, 116, 120, 138, 113, 156, 168, 122, 121, 172, 137, 174, 152, 154, 129, 126, 146, 160, 170, 115, 159, 232, 162, 194, 186, 141, 135, 158, 125, 210, 204, 164, 149, 200, 153, 176, 216, 180, 151, 188, 143, 136, 119, 246, 218, 165, 147, 184, 167, 196, 228, 161, 127, 182, 155, 224, 234, 198, 214, 212, 177, 226, 258, 192, 294, 206, 171, 208, 173, 191, 342, 202,...

Example:

The initial 0 above is part of six 3-term alignments of neighboring terms, situated on a diagonal.

The "/" alignements are:

22+7+0=29 (a prime);

7+0+4=11;

0+4+27=31.

The "\" alignements are:

20+9+0=31;

9+0+2=11;

0+2+11=13; etc.

The variant where the six such alignments add up to a square instead of a prime (like above) needs a lot of backtrack — and was thus halted after a few terms:

S3Xsq = 0, 1, 2, 3, 4, 5, 7, 6, 12, 21, 8, 9, 14, 17, 15, 32, 45, 25, 30, 28, 18, 29, 44, 38, 13, 27, 26, 230, 16, 39, 20,...

______________________________________________________________________________________________________

And more (from Carole):

«Spiral on a 2D square lattice, one term per cell, starting at the origin with 0; the four integers at the corners of any 3x3 square add up to a square»:

S33Sq = 0, 1, 2, 3, 4, 5, 6, 7, 13, 8, 9, 18, 10, 11, 17, 19, 12, 14, 20, 25, 15, 16, 29, 27, 26, 21, 22, 32, 44, 37, 23, 24, 31, 36, 63, 28, 30, 33, 47, 43, 64, 57, 34, 35, 40, 54, 41, 52, 45, 38, 39, 46, 70, 49, 55, 53, 42, 48, 62, 73, 80, 66, 60, 51, 50, 56, 74, 71, 90, 59, 100, 77, 58, 61, 83, 91, 69, 122, 72, 86, 88, 65, 67, 84, 155, 119, 68, 101, 121, 103, 75, 76, 105, 136, 97, 93, 98, 99, 133, 106, 78, 79, 120, 126, 92, 87, 158, 102, 144, 104, 81, 82, 141, 95, 109, 140, 134, 115, 180, 156, 108, 85, 89, 162, 145, 154, 107, 112, 129, 110, 135, 161, 94, 96, 170, 114, 167, 165, 132, 137, 128, 146, 123, 124, 111, 113, 116, 125, 160, 148, 117, 163, 177, 142, 149, 183, 118, 127, 159, 192, 184, 185, 193, 131, 150, 190, 174, 143, 178, 130, 138, 191, 171, 189, 232, 233, 221, 172, 166, 153, 214, 224, 139, 147, 197, 241, 152, 223, 175, 173, 206, 164, 188, 207, 226, 199, 151, 157, 274, 169, 204,...

Example: 
The initial 0 above is the 4th corner of four 3x3 squares which are:
– the NW square formed by 0,20,15,29 (sum=64, a square);
– the NE square formed by 0,29,26,9 (sum=64);
– the SE square formed by 0,9,10,17 (sum=36);
– the SW square formed by 0,17,12,20 (sum=49); etc.

The same idea hereunder — with primes instead of squares:

«Spiral on a 2D square lattice, one term per cell, starting at the origin with 0; the four integers at the corners of any 3x3 square add up to a prime»:

S33Pr = 0, 1, 2, 3, 4, 5, 6, 7, 11, 8, 9, 13, 10, 12, 18, 19, 14, 15, 21, 16, 17, 20, 23, 27, 29, 22, 24, 33, 30, 25, 26, 28, 31, 35, 34, 36, 32, 37, 39, 40, 48, 38, 41, 42, 44, 62, 46, 50, 56, 43, 45, 66, 54, 52, 58, 64, 47, 49, 76, 51, 53, 55, 72, 68, 57, 59, 80, 63, 78, 69, 65, 70, 60, 61, 81, 74, 90, 102, 85, 82, 92, 67, 71, 86, 88, 98, 87, 73, 84, 94, 75, 77, 96, 100, 104, 106, 108, 116, 83, 120, 79, 89, 99, 113, 93, 91, 97, 112, 95, 126, 101, 103, 110, 122, 118, 105, 109, 114, 136, 124, 134, 107, 111, 115, 119, 123, 129, 132, 138, 125, 130, 117, 121, 127, 133, 131, 141, 128, 139, 145, 137, 151, 135, 149, 140, 142, 147, 146, 155, 153, 144, 148, 152, 156, 154, 150, 143, 157, 164, 159, 158, 163, 162, 160, 166, 165, 178, 173, 176, 161, 167, 168, 169, 170, 171, 187, 175, 183, 177, 191, 185, 181, 172, 174, 199, 179, 193, 201, 184, 180, 197, 205, 189, 190, 196, 195, 182, 186, 202, 207, 213,...

Example:

The initial 0 above is the 4th corner of four 3x3 squares which are:

– the NW square formed by 0,21,17,23 (sum=61, a prime);

– the NE square formed by 0,23,29,9 (sum=61);

– the SE square formed by 0,9,10,18 (sum=37, a prime);

– the SW square formed by 0,18,14,21 (sum=53, a prime); etc.

A last "graphic" fantasy hereunder:

«Lexicographically earliest spiral of distinct nonnegative terms on a 2D square lattice, one term per cell, starting at the origin with 0; the cells containing one ore more 1s cannot touch each other and form a new 2D square lattice»:

S1BLUE = 0,1,2,3,4,10,5,6,7,8,9,20,22,11,23,12,24,25,26,27,28,13,29,14,30,15,32,16,33,17,34,35,36,37,38,39,40,18,42,19,43,21,45,46,47,48,49,50,52,53,54,55,56,57,58,59,31,60,41,62,51,63,61,64,65,66,67,68,69,70,72,73,71,74,81,75,91,76,100,77,101,78,102,79,103,80,104,82,105,83,106,84,107,...

______________________________________________________________________________________________________

Another variant from Carole:

«Lexicographically earliest spiral of distinct nonnegative terms on a 2D square lattice, one term per cell, starting at the origin with 0 such that the 8 cells surrounding any integer sum up to a prime»:

T8pr =

0, 1, 2, 3, 4, 5, 6, 7, 9, 8, 10, 14, 11, 12, 16, 13, 15, 17, 20, 22, 18, 19, 36, 21, 24, 23, 25, 26, 28, 37, 27, 29, 30, 32, 31, 33, 34, 35, 44, 43, 38, 42, 39, 40, 45, 49, 41, 53, 47, 46, 48, 56, 62, 54, 55, 51, 50, 52, 64, 60, 57, 58, 59, 66, 61, 63, 65, 76, 78, 72, 84, 70, 67, 68, 74, 92, 69, 86, 71, 88, 80, 73, 75, 87, 90, 82, 96, 77, 79, 102, 81, 83, 94, 89, 98, 100, 112, 85, 104, 108, 91, 93, 114, 95, 110, 99, 105, 118, 103, 120, 97, 101, 111, 115, 107, 132, 109, 117, 106, 121, 127, 113, 116, 119, 122, 135, 141, 123, 125, 126, 133, 124, 128, 129, 134, 131, 130, 140, 147, 137, 144, 143, 145, 136, 138, 139, 151, 150, 149, 154, 161, 155, 152, 142, 158, 169, 146, 148, 160, 166, 156, 163, 170, 157, 165, 159, 176, 162, 168, 153, 164, 188, 172, 180, 173, 174, 178, 190, 182, 175, 192, 177, 167, 171, 196, 186, 187, 184, 194, 181, 189, 193, 200, 202, 179, 185, 183, 191, 197, 204, 199,...

Example:

– the 8 terms surrounding the initial zero are 1,2,3,4,5,6,7,9 with sum 37 (a prime);

– the 8 terms surrounding 11 (two diagonal steps towards SE from 0) are 2,14,28,37,27,29,30,12 with sum 179 (a prime);

– the 8 terms surrounding 15 (two diagonal steps towards SW from 0) are 4,13,31,33,34,35,44,17 with sum 211 (a prime); etc.

______________________

And this variant, of course, with the squares (instead of the primes):

T8sq = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 25, 11, 12, 19, 21, 13, 14, 46, 20, 15, 16, 35, 29, 30, 17, 18, 31, 27, 50, 22, 23, 64, 49, 41, 26, 24, 28, 38, 70, 39, 59, 32, 33, 51, 58, 81, 61, 66, 34, 36, 107, 84, 44, 69, 68, 37, 40, 63, 62, 85, 57, 54, 86, 42, 43, 108, 95, 67, 122, 130, 93, 45, 47, 154, 110, 155, 52, 109, 100, 97, 48, 53, 112, 77, 201, 71, 92, 202, 113, 55, 56, 120, 140, 105, 96, 102, 76, 72, 104, 60, 65, 75, 101, 80, 133, 99, 79, 153, 131, 73, 74, 126, 119, 158, 172, 159, 166, 156, 152, 175, 78, 82, 170, 150, 157, 114, 187, 233, 87, 142, 137, 83, 88, 128, 148, 117, 129, 149, 211, 296, 146, 220, 209, 89, 90, 205, 165, 171, 163, 123, 151, 219, 189, 138, 135, 91, 94, 192, 253, 272, 176, 286, 200, 229, 291, 225, 204, 203, 98, 103, 111, 162, 182, 243, 217, 143, 298, 145, 144, 141, 134, 106, 115, 124, 263, 235, 237, 255, 197, 274, 179, 236, 186, 212, 195, 116, 118, 369, 181, 364,...

Example:

– the 8 terms surrounding the initial zero are 1,2,3,4,5,6,7,8 with sum 36 (a square);

– the 8 terms surrounding 11 (two diagonal steps towards SE from 0) are 2,25,27,50,22,23,64,12 with sum 225 (the square of 25);

– the 8 terms surrounding 13 (two diagonal steps towards SW from 0) are 4,21,41,26,24,28,38,14 with sum 196 (the square of 14); etc.

______________________________________________________________________________________________________

More submissions coming soon (?)

The hereunder nice "spiral" pix are taken from the opening titles' sequence of Charade, the wonderful 1963-film by Stanley Donen shot in Paris with Audrey Hepburn, Cary Grant, Walter Matthau, James Coburn, etc.