A self-trapped sum?

We start our journey on a grid plane, marking 1 in a cell.
At every step we write the next natural integer in an empty cell.
This empty cell must be one of the 8 cells in contact with the last marked one.
(Those 8 cells form what we call a square “crown”.)
Here is our only rule, in three parts:
 
— If the sum of the last two integers marked on the grid is prime, write the next integer in the crown’s cell that is the furthest from the cell 1;
— If the sum is not prime, write the next integer in the crown’s cell that is the closest to the cell 1;
— If more than one cell of the crown is available (and valid), pick up the one you wish.  

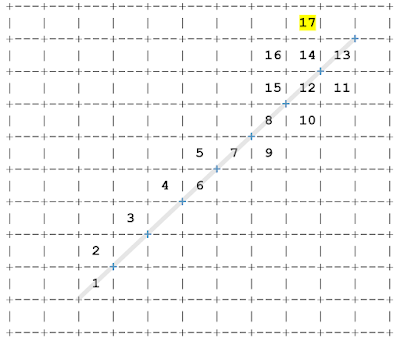
As the sum of the last two integers marked on the grid is not prime we place 2 somewhere in the “crown” – but close to 1 (the yellow 2 cell hereunder is geometrically closer to 1 then the “x” cell) :

The sum 1+2 is prime, mark 3 as indicated below (the alternative and valid cell for 3 is in red):

The sum 2+3 is prime (go away!), mark 4 as indicated below (we have highlighted a diagonal passing through the cell 1):

The sum 3+4 is prime (go away!), mark 5 as indicated below:

The sum 4+5 is not prime (zurück!), mark 6 as indicated below:

The sum 5+6 is prime (go away!), mark 7 as indicated below:

The sum 6+7 is prime (go away!), mark 8 as indicated below:

The sum 7+8 is not prime (zurück!), mark 9 as indicated below (or in the red cell):

The sum 8+9 is prime (go away!), mark 10 as indicated below:

The sum 9+10 is prime (go away!), mark 11 as indicated below:

The sum 10+11 is not prime (zurück!), mark 12 as indicated below:

The sum 11+12 is prime (go away!), mark 13 as indicated below:

The sum 12+13 is not prime (zurück!), mark 14 as indicated below:

The sum 13+14 is not prime (zurück!), mark 15 as indicated below:

The sum 14+15 is prime (go away!), mark 16 as indicated below:

The sum 15-16 is prime (go away!), mark 17 as indicated below:

The sum 16+17 is not prime (zurück!), mark 18 as indicated below:

 

The sum 17+18 is not prime (zurück!), mark 19 as indicated below:

The sum 18+19 is prime (go away!), mark 20 as indicated below:

The sum 19+20 is not prime (zurück!), mark 21 as indicated below:

The sum 20+21 is prime (go away!), mark 22 as indicated below:

The sum 21+22 is prime (go away!), mark 23 as indicated below:

The sum 22+23 is not prime (zurück!), mark 24 as indicated below:

Etc.

Question
I would like to self-trap myself: is it possible?
Best,
É.
(hope this idea is not old hat – and that I did not leave too many mistakes above).

_______

Update, May 21st 2021

The answer is yes

Here are the comments made by Scott Shannon and Maximilian Hasler (in private and on Math-Fun):

[Scott Shannon]
... ' pick up the one you wish.'
 
The ambiguity comes when a number is on one of the diagonal lines (like the number 8) and two squares the same distance from 1 can be chosen.  E.g. the number 9 can be picked to be directly below it (i.e. closest to the x-axis) or to the left of it (closest to the y-axis). The choice matters as the visited squares are not symmetrical so the choice affects the resulting path. As you can see from my two results the path is different depending on what axis you choose to go toward when there is a choice.

 
[Maximilian Hasler]
Eric,
one more nice idea! I was about to criticize the "pick the one you wish"
clause for making the solution "ill defined",
when I understood that this leads to the whole, maybe infinite set of
distinct solutions we have to consider.
To answer your question whether this set has a "finite" solution in the
sense that it can't be extended beyond a given point:
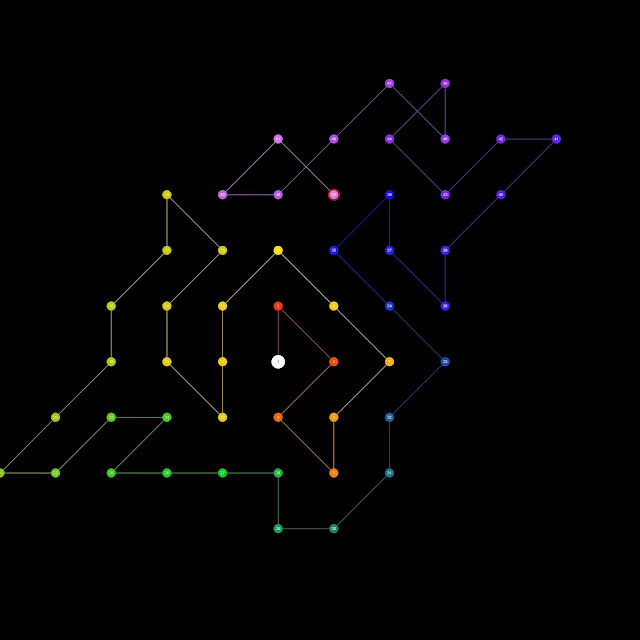
Yes, consider the following one, stuck after move 115:
[reformat the following lines in "fixed width" if this formatting got lost]

(Start and end bold+yellow marks by me, Eric A.)

Here the choice was made by PARI's default comparison function, used to
sort the possible destinations according to the distance from the origin
and then according to the position, written as complex numbers x+iy -- I
don't know how PARI compares these.
For prime sums n+(n-1) I chose the last, else the first among the possible
destinations sorted that way.
 
- Maximilian
 
(PARI)
/* Compute the sequence. Remove "0&&" to print the sequence as "a(n) =
X+I*Y". */
{pos=0; grid=Map(); for(n=1,199, mapput(grid, pos, n); L=List(); for(x=-1,1,
  forstep( y=-1,1,1+!x, mapisdefined(grid, pos+x+I*y)|| listput(L, [norm(
pos+x+I*y), x+I*y ]) ));
#L||return(n); listsort(~L); pos+= L[ if( isprime( n*2-1),#L, 1) ][2] ; 0&&
printf("a(%d)=%s, ",n, pos))}
/* display the grid: */
foreach(Set(imag( pos=Set(Mat(grid)[,1]) )),y, foreach(Set(real(pos)),x,
printf("%4d",iferr(mapget(grid,x+I*y),E,)));print)

[Scott again, a few hours later]:

Here's another one which, if the distances from 1 are equal for two squares, It chooses the one which itself has the fewest visited neighbours. This is nice as no 'third level' deciding is needed... i.e. needing to use the minimum neighbour count is only used 3 times, and each time there is a definite minimum so we don't need a third level of decision. Only problem is the walk is quite short! :)

Note: this has a clear decision for the 8-choosing-9 square.... going straight down only has 7 as a neighbour, while going left gives both 5 and 7 as neighbours, so it chooses to go straight down.

(...) After sending the rule I mentioned to you (go to the square which has the fewest neighbors) I added an addition tiebreaker that, if two squares have the same min neighbor count, go to the one that has the minimum sum of the values in its neighboring squares.  Not needed for your prime question as the min-neighbor count is sufficient tiebreaker as my latest image showed.

But I thought.... hmm, there are not a lot of primes so the path goes inward most of the time, hence it gets trapped. What other ways are there to sort the numbers into a group that has more members than the primes? I then thought of 'lets sum the numbers as we go, and then take that sum mod X .... if that is zero, step away, else step inward'. Of course X is arbitrary, and that’s where the fun begins. There's obviously limitless ways to filter out the number here, but I just started with the mod idea!

I've done X from 2 to 50, and the really good news is... the above two rules are sufficient to unambiguously pick the next square. I have a fourth level 'choose one closest to the x-axis'... but it is never used! Well not for X up to 50, so the walks one generates are 'pure', without any arbitrary direction picking. Nice!

Anyway for X = 2,3 and 5, the path is... infinite. The path forms a repeating pattern moving away from the center. See attaching images. The path for X=2 is very very cool!  What a great way to make a spiral. And what makes it especially nice is that the path is decide only using the min-neighbour count rule.. the neighbour sum is never needed either.

For all other numbers the path gets trapped.  For X=2..50 the faster is X=10 which gets trapped after 52 steps, the longest is 32, which takes 5171 steps.  See attaching images. Also attaching X=4.  This now reminds me of the trapped night sequences.... so many variations and you never know what you'll get when you change the rules! I think you may have started a whole new area of fun walks :)

Many thanks, folks across the universe (La Martinique and Australia)!