Peindre avec des nombres

Ce beau paysage (dû ici à Hans Havermann, et plus bas aux 100000 termes de Jean-Marc Falcoz) s'obtient en faisant le graphe d'une fonction toute simple :
Commencer la suite S avec a(1) = 1 ;
Étendre S avec le plus petit nombre non encore présent dans S qui permette de former un palindrome.
Le palindrome s'obtient en ajoutant les termes impairs et en soustrayant les pairs.

 La suite S commence par : 
S = 1, 3, 2, 5, 4, 19, 11, 22, 6, 17, 14, 8, 7, 15, 16, 27, 24, 13,...


Les "sommes" cumulées sont mises en regard ci-dessous, avec la ligne P (pour Palindrome) et l'opération pratiquée (plus ou moins)  :
       +  -  +  -   +   +   -  -   +   -  -  +   +   -   +   -   +
S = 1, 3, 2, 5, 4, 19, 11, 22, 6, 17, 14, 8, 7, 15, 16, 27, 24, 13, ...
P = 1  4  2  7  3  22  33  11  5  22   8  0  7  22   6  33   9  22 ...

 Les palindromes ne peuvent être négatif, évidemment (le plus petit est zéro).

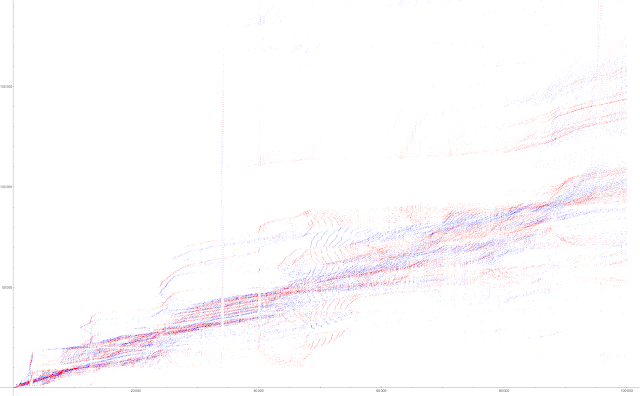
 Voici le graphe de Jean-Marc, c'est une tuerie de strates et de drapés, merci à lui !
Tout ceci sera bientôt dans l'OEIS, là (et ici pour la suite où l'on permute dans la définition les mots "pairs" et "impairs")

Commentaires

Enregistrer un commentaire

Posts les plus consultés de ce blog

Beautés ?

Image
Beau comme un clavier ? Un deuxième ? (celui de Modotti)   Beau comme le dos d ’ un timbre proposé par Delcampe ? Beau comme une série ukrainienne où les avions râpent le Kremlin ? Belle comme Chargois ? ... belle comme Germaine Richier ? Bel atelier ? Beau comme une pièce de 1 santim ? ... ou comme une pièce de 50  santeem ? ... Byrrh , beau comme un anus ? Beau comme la collection de Marin Karmitz à Beaubourg ? Belles Ménines ? Beau comme Marcel Duchamp ? Beau comme Jean-Luc Godard ? Beau comme la réouverture de l ’ Einsteinturm à Berlin ? Beau comme un anneau dudit ? Beau comme Eisenstein ? Beau comme les fleurs de Pascale hier matin ? Beau comme on dirait la planète Mars ? Beau comme des recherches personnelles ? Beau comme une marelle (vers le ciel) ? Beau comme un triple selfie (au Man Ray ) ? Beau comme le ciel de Sacha , mardi, en face du restaurant La Montagne ? (qui a rouvert) ... beau comme ce bleu-là de Lo ? Beau comme le froid ? Beau comme une Vespa ? Beau comme Cloon
Lire la suite

Underline, reproduce

Image
Dall.e creation If we underline the... « first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, tenth, eleventh,… » letter of this sentence S 1 , we see that the successive underlined letters simply reproduce S 1 . No big deal. If we decide not to start S 1   with "first" but with "sixth", we can reproduce the new S 6  quite easily: S 6 = sixth , second, third, fourth, fifth, first , seventh, eighth, ninth, tenth, eleventh,… S 6  was reproduced in a slightly less mechanical manner than  S 1 :  just two words of  S 1   swapped here ("first" and "sixth", in red, above). If we start S 8  with "eighth" we just swap again a pair of words of S 1  ("first" and "eighth", in red, hereunder): S 8  = eighth , second, third, fourth, fifth, sixth, seventh, first , ninth, tenth, eleventh,… What about starting S 9  with "ninth"? How many swaps do we need to reproduce S 9 ?  This is more tricky! (Indeed, we
Lire la suite

Le tripalin se présente

Image
Un tripalin est constitué de trois images. Chaque image illustre un substantif. Accolés, ces trois substantifs forment une chaîne palindromique. Laquelle nous vous invitons à trouver.  Exemple ci-dessous. Le premier mot est COL-BLEU Le second DUEL Le troisième BLOC . Ces mots forment la chaîne COLBLEUDUELBLOC qui est bien palindromique. Je posterai chaque jeudi une nouvelle salve de tripalins . Rien que des noms illustrés – pas d’adjectifs, pas de verbes conjugués, pas d’adverbes (parfois un prénom ou un nom propre – mais seulement quand il faut). À la demande générale (de mon neveu), chaque tripalin sera surmonté de son numéro d ’ ordre ( octothorpe noir) et de trois nombres bleus. Ces nombres reprennent les trois longueurs (en lettres) des trois mots présents dans le tripalin. On a par exemple ci-dessous [ #0 ↓ 7+4+4 ] car COL-BLEU comporte  7  lettres, DUEL   4  et BLOC   4 . Le numéro d ’ ordre est zéro. #0 ↓ 7+4+4 Voilà – tous retours critiques, construits ou déconstruits, bien
Lire la suite