Two identical digits
There are at least 2 identical digits in the result of a(n) * a(n+1). This is the lexicographically earliest sequence of distinct positive terms with this property (I hope).
S = 1,11,2,22,3,33,10,20,5,23,7,16,9,13,17,15,35,19,6,24,12,21,25,4,28,8,...
Examples
1 * 11 = 11
11 * 2 = 22
2 * 22 = 44
22 * 3 = 66
3 * 33 = 99
33 * 10 = 330
10 * 20 = 200
20 * 5 = 100
5 * 23 = 115
7 * 16 = 112
Etc.
____________________
Around midnight update
> Giorgos Kalogeropoulos was quick to compute S; here are the first 100 terms:
S = 1, 11, 2, 22, 3, 33, 10, 20, 5, 23, 7, 16,
9, 13, 17, 15, 35, 19, 6, 24, 12, 21, 25, 4, 28, 8, 14, 18, 29, 31, 32, 34, 26,
38, 30, 36, 37, 27, 40, 45, 39, 41, 42, 44, 46, 47, 43, 52, 50, 48, 49, 51, 59,
56, 55, 57, 58, 54, 53, 61, 60, 65, 62, 67, 63, 68, 66, 64, 69, 71, 72, 70, 73,
75, 74, 78, 77, 76, 79, 81, 82, 80, 83, 85, 89, 84, 86, 90, 92, 87, 88, 91, 94,
97, 100, 93, 95, 101, 96, 102, ...
> I didn't send a plot because it soon becomes a straight line. I will try some variations.
GK
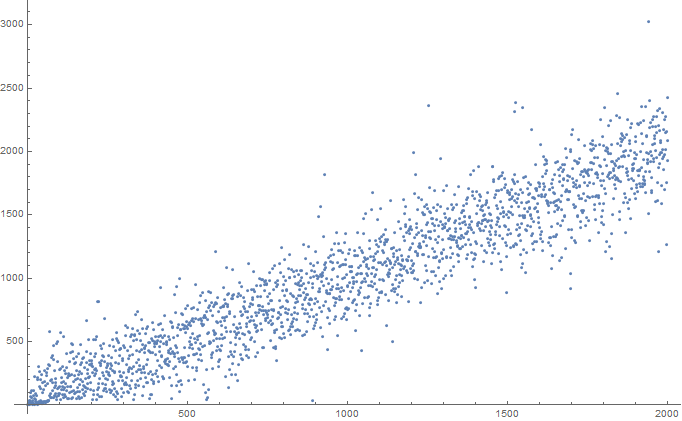
How about T: Every digit has a twin (first 100 terms hereunder and graph of the first 1000 terms):
T = 1, 11, 2, 22, 3, 33, 34, 66, 17, 101, 10, 110, 20, 55, 21, 132, 9, 202, 5, 220, 15, 77, 13, 88, 24, 176, 12, 99, 19, 121, 28, 143, 7, 165, 27, 44, 25, 209, 16, 187, 6, 198, 14, 242, 23, 303, 4, 275, 8, 264, 32, 3159, 154, 18, 253, 29, 231, 26, 297, 364, 286, 31, 319, 314, 415, 294, 429, 238, 572, 182, 561, 200, 583, 190, 739, 155, 658, 246, 407, 276, 363, 277, 578, 279, 390, 295, 374, 273, 385, 288, 351, 308, 338, 461, 333, 341, 339, 298, 396, 278, ...
First 1000 terms of T
First 3000 terms of T
GK
This sequence is finite: the largest product of 2 successive terms is 99887766554433221100. So, the divisors of this products (namely the terms of this sequence) are finite. If we want another variation with infinite terms (sequence U hereunder), we should ask that "We have at least 2 digits of every digit in a(n) * a(n+1)". The first 100 terms of U are:
U = 1, 11, 2, 22, 3, 33, 34, 66, 17, 101, 10, 110, 20, 55, 21, 37, 6, 74, 9,
111, 4, 222, 50, 44, 25, 88, 13, 77, 15, 202, 5, 220, 30, 303, 7, 143, 8, 264, 16,
132, 32, 198, 14, 242, 23, 99, 12, 176, 19, 121, 28, 275, 24, 187, 18, 154, 26,
231, 29, 253, 35, 165, 27, 286, 31, 319, 38, 307, 76, 579, 57, 193, 89, 199, 56,
377, 112, 387, 178, 471, 358, 59, 274, 73, 137, 87, 153, 174, 209, 42, 481, 63,
497, 126, 344, 71, 141, 93, 282, 142, ...
Graph of the first 3000 terms of UÉA
> Many thanks, Giorgos, good job and interesting variations!
____________________
Next day update
Jean-Marc Falcoz proposed another variation leading to a finite sequence (X, first 113 terms below):
"Lexicographically earliest sequence of distinct positive terms such that a(n)*a(n+1) contains exactly 1 digit 1 (if 1 is present), 2 digits 2 (if 2 is present), 3 digits 3 (if 3 is present)... 9 digits 9 (if 9 is present)." The sequence is finite as the largest possible product a(n)*a(n+1) is 999999999888888887777777666666555554444333221.
X = {1,22,202,130033,1942165,285373,15637242,2715027,1235905,28677249,1832656,13337667,1840302,13218127,32769805,13257151,12564203,2740608,9287193,778209,8253074,2972871,1270532,58383242,4563358,30184653,110706148,3120274,23859178,18217997,11831885,19654883,73038,45748,772824,30324531,536086,1028854,647579,687569,2099505,12067389,3691397,1751712,10406299,5316246,6479112,857237,4837218,321163,13561818,3335508,7056003,6427485,5046197,12810922,40711,103494,41881,103224,32206,131439,16306,252939,215286,8005062,6913557,4849085,7099371,4863044,503106,6389,4906,135887,38659,91967,386565,117585,208823,2181485,10746603,319308761,163341483,22795339,14571196,10597864,22884946,19341827,11718979,3708117,9318866,7142667,7365968,11293599,4635675,6999079,647736,7203809,3397886,7223769,3120747,8176448,27845437,19947733,22826425,10582189,6091997,12214841,1992294,11823328,37926571,34974516,66380809,...}
We have indeed:
1
* 22 = 22
22
* 202 = 4444
202 * 130033
= 26266666
130033 * 1942165
= 252545541445
1942165 * 285373
= 554241452545
285373 * 15637242
= 4462446661266
15637242 * 2715027
= 42455534235534
2715027 * 1235905
= 3355515444435
1235905 * 28677249
= 35442355425345
28677249 * 1832656
= 52555532443344
1832656 * 13337667
= 24443355453552
13337667 * 1840302
= 24545335255434
1840302 * 13218127
= 24325345554354
13218127 * 32769805
= 433155444255235
32769805 * 13257151
= 434434253125555
13257151 * 12564203
= 166565536365653
12564203 * 2740608
= 34433555255424
2740608 * 9287193
= 25452555433344
9287193 * 778209 = 7227377177337
778209 * 8253074
= 6422616464466
8253074 * 2972871
= 24535324355454
2972871 * 1270532
= 3777127737372
1270532 * 58383242
= 74177777224744
58383242 * 4563358
= 266423634446636
4563358
* 30184653 = 137743377744774
30184653 * 110706148
= 3341626662346644
110706148 * 3120274 = 345433515244552
3120274 * 23859178 = 74447172774772
23859178 * 18217997 = 434666433226466
18217997 * 11831885 = 215553245434345
11831885 * 19654883 = 232554315344455
19654883
* 73038 = 1435553344554
73038
* 45748 = 3341342424
45748
* 772824 = 35355152352
772824 * 30324531 = 23435525345544
30324531 * 536086 = 16256556525666
536086
* 1028854 = 551554225444
1028854
* 647579 = 666264244466
647579
* 687569 = 445255245451
687569
* 2099505 = 1443554553345
2099505 * 12067389 = 25335543542445
12067389 * 3691397 = 44545523552433
3691397
* 1751712 = 6466264421664
1751712 * 10406299 = 18228838833888
10406299 * 5316246 = 55322445433554
5316246 * 6479112 = 34444553253552
6479112 * 857237 = 5554134533544
857237 * 4837218 = 4146642246666
4837218 * 321163 = 1553535444534
321163 * 13561818 = 4355554154334
13561818 * 3335508 = 45235552433544
3335508
* 7056003 = 23535354454524
7056003 * 6427485 = 45352353442455
6427485
* 5046197 = 32434355524545
5046197
* 12810922 = 64646436163634
12810922 * 40711 = 521545445542
40711 * 103494 = 4213344234
103494 * 41881 = 4334432214
41881 * 103224 = 4323124344
103224 * 32206 = 3324432144
32206 *
131439 = 4233124434
131439
* 16306 = 2143244334
16306
* 252939 = 4124423334
252939
* 215286 = 54454225554
215286
* 8005062 = 1723377777732
8005062 * 6913557 = 55343452425534
6913557 * 4849085 = 33524425545345
4849085
* 7099371 = 34425453425535
7099371
* 4863044 = 34524553545324
4863044 * 503106 = 2446626614664
503106
* 6389 = 3214344234
6389
* 4906 = 31344434
4906
* 135887 = 666661622
135887 * 38659 = 5253255533
38659 *
91967 = 3555352253
91967 *
386565 = 35551223355
386565
* 117585 = 45454245525
117585
* 208823 = 24554452455
208823
* 2181485 = 455544242155
2181485
* 10746603 = 23443553245455
10746603 * 319308761
= 3431484488888883
319308761 * 163341483 = 52156366556632563
163341483 * 22795339
= 3723424477747737
22795339 * 14571196
= 332155352455444
14571196 * 10597864
= 154423553525344
10597864 * 22884946
= 242531545355344
22884946 * 19341827
= 442636666436342
19341827 * 11718979
= 226666464434633
11718979 * 3708117
= 43455345252543
3708117 * 9318866
= 34555445435322
9318866 * 7142667
= 66561556655622
7142667 * 7365968
= 52612656556656
7365968 * 11293599
= 83188288838832
11293599 * 4635675
= 52353454544325
4635675 * 6999079
= 32445455543325
6999079 * 647736
= 4533555435144
647736 * 7203809
= 4666166426424
7203809 * 3397886
= 24477721747774
3397886 * 7223769
= 24545543552334
7223769 * 3120747
= 22543555435443
3120747 * 8176448 = 25516625566656
8176448
* 27845437 = 227676767667776
27845437 * 19947733 = 555453342544321
19947733 * 22826425 = 455335431244525
22826425 * 10582189 = 241553543544325
10582189 * 6091997 = 64466663641433
6091997 * 12214841 = 74412774727477
12214841 * 1992294 = 24335554435254
1992294 * 11823328 = 23555545434432
11823328 * 37926571 = 448418288848288
37926571 * 34974516 = 1326463464264636
34974516 * 66380809 = 2321636666463444
Merci Jean-Marc ! We love those "monsters"!
(pix taken from here)







Commentaires
Enregistrer un commentaire