Le monde selon les lois de Marf-Low

Je viens de poster ce message sur le forum Math-Fun (et vous devinez d'où vient le nom du créateur de ces lois) :
A Marf-Low rule is coded in a 3-digit base-10 integer abc where neither a nor b = 0.
A sequence of integers is then produced with this rule.
The abc integer is interpreted like this:
a = a(1) [taken in the set 1,2,3,4,5,6,7,8,9]
b = a multiplicative factor [taken in the same set]
c = a stop-digit [taken in the set 1,2,3,4,5,6,7,8,9,0].
Example:
The Marf-Low rule 173 produces the seq:
S = 1, 7, 49, 343, 2, 14, 98, 686, 4802, 33614, 3, 4, 28, 196, 1372, 5, 35, 6, 42, 296,...
Explanation:
# Start the seq with a(1) = a [here a(1) = 1]
# If a(n) doesn't show the stop-digit c, then a(n+1) = 7*a(n) [this is the case here, as 1, not showing any digit 3, is then multiplied by 7, producing a(2) = 7]
# else a(n+1) is the smallest integer not yet in the sequence [we will see this below].
The rule 173 produces indeed 1, 7, 49, 343 which stops and restarts with 2, 14, 98, 686, 4802, 33614 which stops and restarts with 3 which stops and restarts with 4, 28, 196, 1372 which stops and restarts with 5, 35 which stops, etc.
Which Marf-Low rule (from 110 to 999) produces the nicest 10,000-point graph, according to you?
Best,
É.
_______________________________________________
math-fun mailing list
math-fun@mailman.xmission.com
_______________________________________________
Jean-Marc Falcoz me répondit pendant la nuit en calculant les graphes des premières Marf-Low rules allant de 110 à 250.
Ainsi les 50 premiers termes de la rule 173 ci-dessus sont-ils :
M(173) = 1, 7, 49, 343, 2, 14, 98, 686, 4802, 33614, 3, 4, 28, 196, 1372, 5, 35, 6, 42, 294, 2058, 14406, 100842, 705894, 4941258, 34588806, 8, 56, 392, 9, 63, 10, 70, 490, 3430, 11, 77, 539, 12, 84, 588, 4116, 28812, 201684, 1411788, 9882516, 69177612, 484243284, 13, 15,...
Le plus grand des 10000 premiers termes de la suite M(173) est 4943316857500. Il s'obtient après 11 multiplications successives par 7 du terme 2500, multiplications où n'apparaît jamais le chiffre 3 (sauf à la fin) :
2500 x 7 = 17500 <-- no "3"
17500 x 7 = 122500 <-- no "3"
122500 x 7 = 857500 <-- no "3"
857500 x 7 = 6002500 <-- no "3"
6002500 x 7 = 42017500 <-- no "3"
42017500 x 7 = 294122500 <-- no "3"
294122500 x 7 = 2058857500 <-- no "3"
2058857500 x 7 = 14412002500 <-- no "3"
14412002500 x 7 = 100884017500 <-- no "3"
100884017500 x 7 = 706188122500 <-- no "3"
706188122500 x 7 = 4943316857500 STOP "3"
Rappelons que quand les multiplications s'arrêtent (comme ici), la suite reprend avec le plus petit entier absent de la suite elle-même – lequel sera multiplié par 7, etc.
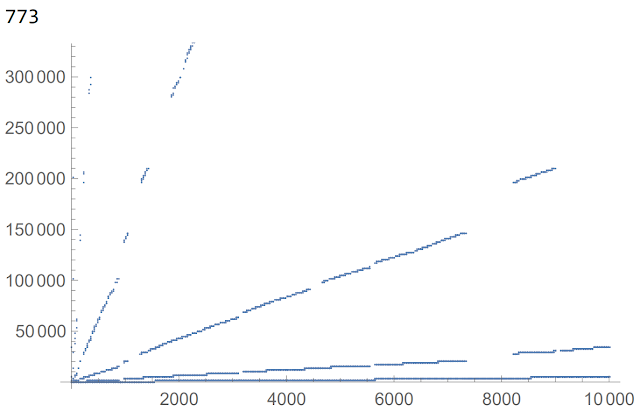
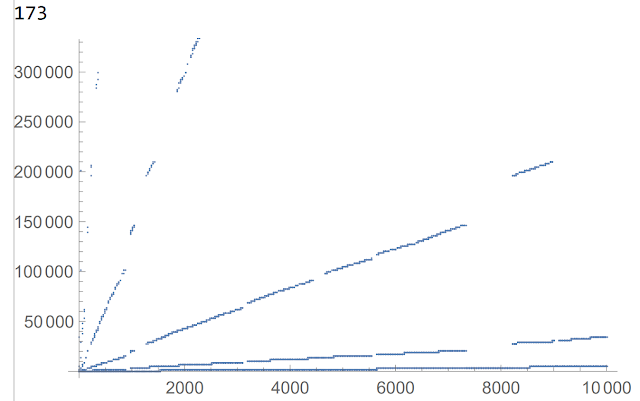
Voici le graphe que dessinent les 10000 premiers termes de M(173) : ils semblent grossièrement se disposer le long de cinq droites :
Ci-dessous, les 50 premiers termes et le graphe de la suite M(135), calculés par Jean-Marc Falcoz :
M(135) = 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 2, 6, 18, 54, 4, 12, 36, 108, 324, 972, 2916, 8748, 26 244, 78 732, 236 196, 708 588, 5, 7, 21, 63, 189, 567, 8, 24, 72, 216, 648, 1944, 5832, 10, 30, 90, 270, 810, 2430, 7290, 21 870, 65 610, 11, 33, 99,...
Le plus grand des 10000 premiers termes de la suite M(135) est 60652829889. Il s'obtient après 16 multiplications successives par 3 du terme 1409, multiplications où n'apparaît jamais le chiffre 5 (sauf à la fin) :
1409 x 3 = 4227 <-- no "5"
4227 x 3 = 12681 <-- no "5"
12681 x 3 = 38043 <-- no "5"
38043 x 3 = 114129 <-- no "5"
114129 x 3 = 342387 <-- no "5"
342387 x 3 = 1027161 <-- no "5"
1027161 x 3 = 3081483 <-- no "5"
3081483 x 3 = 9244449 <-- no "5"
9244449 x 3 = 27733347 <-- no "5"
27733347 x 3 = 83200041 <-- no "5"
83200041 x 3 = 249600123 <-- no "5"
249600123 x 3 = 748800369 <-- no "5"
748800369 x 3 = 2246401107 <-- no "5"
2246401107 x 3 = 6739203321 <-- no "5"
6739203321 x 3 = 20217609963 <-- no "5"
20217609963 x 3 = 60652829889 STOP "5"
Le graphe de M(135) :
Update du 16 octobre avec ce courrier de Jean-Marc Falcoz :
> Salut Eric,
J'ai encore un peu regardé ce matin ces suites.
1) Que se passe-t-il quand on ne fait varier qu'un seul des chiffres ?
Par exemple pour 173 on les 3 possibilités d'évolution :
170, 171, 172, 173, 174, 175, 176, 177, 178, 179
Logiquement, la variation du premier chiffre ne fournit pratiquement pas de changement dans le graphe des 10000 premiers termes.
Par contre, changer le facteur multiplicatif (comme ci-dessous), alors là, c'est un feu d'artifice de changements :
Et finalement, changer le "chiffre interdit" donne quelques changements, mais pas tant que ça. D'ailleurs, assez logiquement, on a plus de variété en changeant du 0 au 1 , ou du 1 au 2, qu'en changeant du 8 au 9 par ex.
2) J'ai regardé le maximum absolu des termes en parcourant 10000 termes de toutes les suites (110 à 999). On a un "phénomène" en partant de 159 : 41503906250000000 (17 chiffres ! Comment est-ce possible ?) Si on regarde sa provenance, on a :
...6793750 (qui contient un 9),
2176,
10880,
54400,
272000,
1360000,
6800000,
34000000,
170000000,
850000000,
4250000000,
21250000000,
106250000000,
531250000000,
2656250000000,
13281250000000,
66406250000000,
332031250000000,
1660156250000000,
8300781250000000,
41503906250000000, (qui contient un 9)
...
Tout vient de 2176, qui est 2^7 * 17 , donc 7 fois de suite, quand on multiplie par 5, on ajoute obligatoirement un 0, et du coup ça laisse un peu moins de chance à un 9 d'apparaître. Ça me plait bien tout ça !
Dans le même 159, on trouve par exemple un autre très joli parcours en partant de 2048=2^11, donc 11 ajouts consécutifs d'un 0 :
...
1279375(qui contient un 9)
2048,
10240,
51200,
256000,
1280000,
6400000,
32000000,
160000000,
800000000,
4000000000,
20000000000,
100000000000,
500000000000,
2500000000000,
12500000000000,
62500000000000,
312500000000000,
1562500000000000,
7812500000000000,
39062500000000000,(qui contient un 9)
...
Sehr schön :o)
Tout de bon
__________________________
Merci Jean-Marc – fascinant (et bien expliqué) en effet !































Commentaires
Enregistrer un commentaire